题目内容
【题目】对于函数y=f(x),若在其定义域内存在x0,使得x0f(x0)=1成立,则称函数f(x)具有性质M.
(1)下列函数中具有性质M的有____
①f(x)=﹣x+2
②f(x)=sinx(x∈[0,2π])
③f(x)=x![]() ,(x∈(0,+∞))
,(x∈(0,+∞))
④f(x)![]()
(2)若函数f(x)=a(|x﹣2|﹣1)(x∈[﹣1,+∞))具有性质M,则实数a的取值范围是____.
【答案】①②④ a![]() 或a>0
或a>0
【解析】
(1)①因为f(x)=﹣x+2,若存在,则![]() ,解一元二次方程即可.②若存在,则
,解一元二次方程即可.②若存在,则![]() ,即
,即![]() ,再利用零点存在定理判断.③若存在,则
,再利用零点存在定理判断.③若存在,则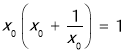 ,直接解方程.④若存在,则
,直接解方程.④若存在,则![]() ,即
,即![]() ,令
,令![]() ,再利用零点存在定理判断.
,再利用零点存在定理判断.
(2)若函数f(x)=a(|x﹣2|﹣1)(x∈[﹣1,+∞))具有性质M,则ax(|x﹣2|﹣1)=1,x∈[﹣1,+∞)有解,将问题转化 :当![]() 时,
时,![]() 有解,当
有解,当![]() 时,
时,![]() 有解,分别用二次函数的性质求解.
有解,分别用二次函数的性质求解.
(1)①因为f(x)=﹣x+2,若存在,则![]() ,
,
即![]() ,所以
,所以![]() ,存在.
,存在.
②因为f(x)=sinx(x∈[0,2π]),若存在,则![]() ,
,
即![]() ,
,
令![]() ,
,
因为![]() ,
,
所以存在![]() .
.
③因为f(x)=x![]() ,(x∈(0,/span>+∞)),若存在,则
,(x∈(0,/span>+∞)),若存在,则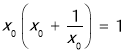 ,
,
即![]() ,所以不存在.
,所以不存在.
④因为f(x)![]() ,(x∈(0,+∞)),若存在,则
,(x∈(0,+∞)),若存在,则![]() ,
,
即![]() ,
,
令![]() ,
,
因为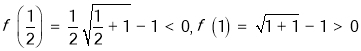 ,
,
所以存在![]() .
.
(2)若函数f(x)=a(|x﹣2|﹣1)(x∈[﹣1,+∞))具有性质M,
则ax(|x﹣2|﹣1)=1,x∈[﹣1,+∞)有解,
当![]() 时,
时,![]() 有解,
有解,
令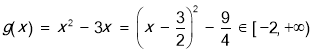 ,
,
所以![]() .
.
当![]() 时,
时,![]() 有解,
有解,
令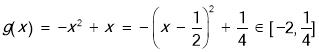 ,
,
所以![]() .
.
综上:实数a的取值范围是a![]() 或a>0.
或a>0.
故答案为:(1). ①②④ (2). a![]() 或a>0
或a>0

练习册系列答案
相关题目


