题目内容
某种商品的价格为每件a元,若涨价x成时,卖出的数量便减少mx成(m为正常数).
(Ⅰ)当m=0.8时,应涨几成价格,才能使售出的商品总金额最大?
(Ⅱ)若适当地涨价,能使销售款增加,那么m的值在什么范围内?
解:(Ⅰ)设卖出b件商品,则售出货款为y=ab.…(1分)
若涨价x成,每件售价为a(1+ )元,卖出了b(1-
)元,卖出了b(1- )件,
)件,
售出总金额为y=ab(1+ )(1-
)(1- ).…(2分)
).…(2分)
当m=0.8时,y=ab(1+ )(1-
)(1-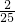 x)=ab[-
x)=ab[- (x-
(x- )2+
)2+ ].…(2分)
].…(2分)
故当x= 时,y取最大值,即涨价125%时,售出的总金额最大.…(2分)
时,y取最大值,即涨价125%时,售出的总金额最大.…(2分)
(Ⅱ)由题意知
化简得:
因为x>0
所以
∴mx<10(1-m)
∴ (m>0)
(m>0)
∴
∴0<m<1
分析:(Ⅰ)某种商品去年售价为每件a元,可售出b件.今年涨价x成(1成=10%),则售出的数量减少mx成(m是正常数).今年该商品售价为每件 ,售出的数量是
,售出的数量是 ,从而可求售出总金额,利用配方法可求其最值;
,从而可求售出总金额,利用配方法可求其最值;
(Ⅱ)原营业额为ab,若是营业额增加只要 的值大于零,从而可求m的范围.
的值大于零,从而可求m的范围.
点评:本题以实际问题为载体,考查函数模型的构建,考查配方法的运用,考查不等式的解法,解题的关键是审清题意,构造函数模型.
若涨价x成,每件售价为a(1+
 )元,卖出了b(1-
)元,卖出了b(1- )件,
)件,售出总金额为y=ab(1+
 )(1-
)(1- ).…(2分)
).…(2分)当m=0.8时,y=ab(1+
 )(1-
)(1-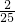 x)=ab[-
x)=ab[- (x-
(x- )2+
)2+ ].…(2分)
].…(2分)故当x=
 时,y取最大值,即涨价125%时,售出的总金额最大.…(2分)
时,y取最大值,即涨价125%时,售出的总金额最大.…(2分)(Ⅱ)由题意知

化简得:

因为x>0
所以

∴mx<10(1-m)
∴
 (m>0)
(m>0)∴

∴0<m<1
分析:(Ⅰ)某种商品去年售价为每件a元,可售出b件.今年涨价x成(1成=10%),则售出的数量减少mx成(m是正常数).今年该商品售价为每件
 ,售出的数量是
,售出的数量是 ,从而可求售出总金额,利用配方法可求其最值;
,从而可求售出总金额,利用配方法可求其最值;(Ⅱ)原营业额为ab,若是营业额增加只要
 的值大于零,从而可求m的范围.
的值大于零,从而可求m的范围.点评:本题以实际问题为载体,考查函数模型的构建,考查配方法的运用,考查不等式的解法,解题的关键是审清题意,构造函数模型.

练习册系列答案
相关题目
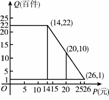
在对口扶贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状态良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型残疾人企业乙,并约定从该店经营的利润中,在保证企业乙的全体职工每月最低生活费的开支3600元后,逐步偿还转让费(不计息),在甲提供资料中:①这种消费品的进价每件14元;②该店月销量Q(百件)与销售单价P(元/件)的关系如右图所示;③该店每月需各种开支2000元。
(1)写出月销量Q(百件)与销售单价P(元/件)的关系,并求该店的月利润L(元)关于销售单价P(元/件)的函数关系式(该店的月利润=月销售利润-该店每月支出);
|
(3)若企业乙只依靠该店,最早可望在多少年后脱贫(无债务)?