题目内容
已知函数 且
且
(Ⅰ)试用含 的代数式表示
的代数式表示 ;
;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)令 ,设函数
,设函数 在
在 处取得极值,记点
处取得极值,记点 ,证明:线段
,证明:线段 与曲线
与曲线 存在异于
存在异于 、
、 的公共点;
的公共点;
【答案】
(Ⅰ)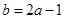 ;(Ⅱ)当
;(Ⅱ)当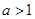 时,函数
时,函数 的单调增区间为
的单调增区间为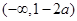 和
和 ,单调减区间为
,单调减区间为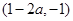 ;当
;当 时,函数
时,函数 的单调增区间为R;当
的单调增区间为R;当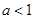 时,函数
时,函数 的单调增区间为
的单调增区间为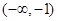 和
和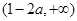 ,单调减区间为
,单调减区间为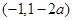
(Ⅲ)易得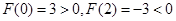 ,而
,而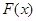 的图像在
的图像在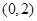 内是一条连续不断的曲线,
内是一条连续不断的曲线,
故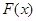 在
在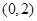 内存在零点
内存在零点 ,这表明线段
,这表明线段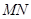 与曲线
与曲线 有异于
有异于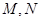 的公共点
的公共点
【解析】
试题分析:解法一:(Ⅰ)依题意,得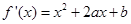
由 得
得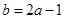
(Ⅱ)由(Ⅰ)得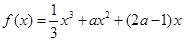
故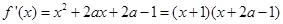
令 ,则
,则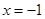 或
或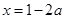
①当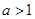 时,
时,
当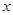 变化时,
变化时,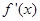 与
与 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
+ |
— |
+ |
|
|
单调递增 |
单调递减 |
单调递增 |
由此得,函数 的单调增区间为
的单调增区间为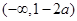 和
和 ,单调减区间为
,单调减区间为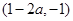
②由 时,
时,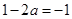 ,此时,
,此时, 恒成立,且仅在
恒成立,且仅在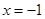 处
处 ,故函数
,故函数 的单调区间为R
的单调区间为R
③当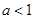 时,
时,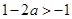 ,同理可得函数
,同理可得函数 的单调增区间为
的单调增区间为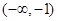 和
和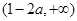 ,单调减区间为
,单调减区间为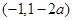
综上:
当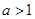 时,函数
时,函数 的单调增区间为
的单调增区间为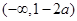 和
和 ,单调减区间为
,单调减区间为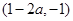 ;
;
当 时,函数
时,函数 的单调增区间为R;
的单调增区间为R;
当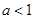 时,函数
时,函数 的单调增区间为
的单调增区间为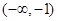 和
和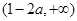 ,单调减区间为
,单调减区间为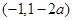
(Ⅲ)当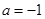 时,得
时,得
由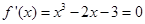 ,得
,得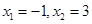
由(Ⅱ)得 的单调增区间为
的单调增区间为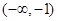 和
和 ,单调减区间为
,单调减区间为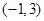
所以函数 在
在 处取得极值。
处取得极值。
故
所以直线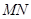 的方程为
的方程为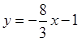
由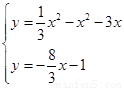 得
得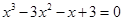
令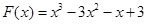
易得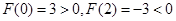 ,而
,而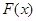 的图像在
的图像在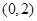 内是一条连续不断的曲线,
内是一条连续不断的曲线,
故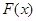 在
在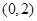 内存在零点
内存在零点 ,这表明线段
,这表明线段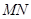 与曲线
与曲线 有异于
有异于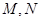 的公共点
的公共点
解法二:
(Ⅲ)当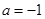 时,得
时,得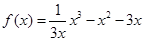 ,由
,由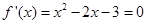 ,得
,得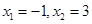
由(Ⅱ)得 的单调增区间为
的单调增区间为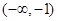 和
和 ,单调减区间为
,单调减区间为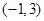 ,所以函数
,所以函数 在
在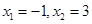 处取得极值,
处取得极值,
故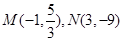
所以直线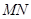 的方程为
的方程为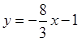
由 得
得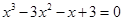
解得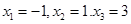
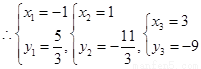
所以线段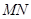 与曲线
与曲线 有异于
有异于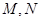 的公共点
的公共点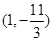 。
。
考点:本题考查了导数的运用
点评:本题是在知识的交汇点处命题,将函数、导数、不等式、方程的知识融合在一起进行考查,重点考查了利用导数研究函数的极值与最值等知识.导数题目是高考的必考题,且常考常新,但是无论如何少不了对基础知识的考查,因此备考中要强化基础题的训练.

练习册系列答案
相关题目

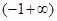
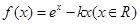
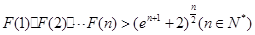 .
.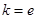 ,试确定函数
,试确定函数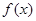 的单调区间;
的单调区间;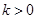 且对任意
且对任意 恒成立,试确定实数
恒成立,试确定实数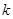 的取值范围;
的取值范围; ,求证:
,求证: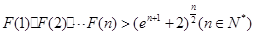 .
.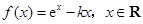
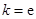 ,试确定函数
,试确定函数 的单调区间;
的单调区间;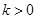 ,且对于任意
,且对于任意 ,
, 恒成立,试确定实数
恒成立,试确定实数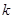 的取值范围;
的取值范围;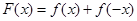 ,求证:
,求证: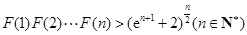 .
.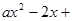 1 .
1 .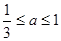 ,且f(x)在区间[1,3]上的最大值为M(a) ,最小值为N(a),
,且f(x)在区间[1,3]上的最大值为M(a) ,最小值为N(a),