题目内容
下列函数中,在其定义域内既是奇函数又是减函数的是
- A.

- B.y=2x
- C.y=x
- D.y=-x3
D
分析:根据奇函数在x=0处函数值为0,得A项不是奇函数,不符合题意;根据指数函数的单调性,得y=2x是R上的增函数,不符合题意;根据函数y=x是R上的增函数,得C项不符合题意;由此可得只有D项符合题意,再利用单调性和奇偶性的定义加以证明即可.
解答:对于A,因为函数 当x=0时,y=sin(-
当x=0时,y=sin(- )≠0
)≠0
所以 不是奇函数,故A项不符合题意;
不是奇函数,故A项不符合题意;
对于B,因为2>1,所以指数函数y=2x是R上的增函数,
不满足在其定义域内是减函数,故B项不符合题意;
对于C,显然函数y=x是R上的增函数,故C项也不符合题意;
对于D,设f(x)=-x3,可得
f(-x)=-(-x)3=x3=-f(x),因此函数y=-x3是奇函数,
又因为f′(x)=-2x2≤0恒成立,可得y=-x3是其定义域内的减函数
∴函数y=-x3是其定义域内的奇函数且是减函数,故D项符合题意
故选:D
点评:本题给出定义在R上的几个函数,要我们找出其中的奇函数且是减函数的函数,着重考查了基本初等函数的单调性与奇偶性及其判断方法的知识,属于基础题.
分析:根据奇函数在x=0处函数值为0,得A项不是奇函数,不符合题意;根据指数函数的单调性,得y=2x是R上的增函数,不符合题意;根据函数y=x是R上的增函数,得C项不符合题意;由此可得只有D项符合题意,再利用单调性和奇偶性的定义加以证明即可.
解答:对于A,因为函数
 当x=0时,y=sin(-
当x=0时,y=sin(- )≠0
)≠0所以
 不是奇函数,故A项不符合题意;
不是奇函数,故A项不符合题意;对于B,因为2>1,所以指数函数y=2x是R上的增函数,
不满足在其定义域内是减函数,故B项不符合题意;
对于C,显然函数y=x是R上的增函数,故C项也不符合题意;
对于D,设f(x)=-x3,可得
f(-x)=-(-x)3=x3=-f(x),因此函数y=-x3是奇函数,
又因为f′(x)=-2x2≤0恒成立,可得y=-x3是其定义域内的减函数
∴函数y=-x3是其定义域内的奇函数且是减函数,故D项符合题意
故选:D
点评:本题给出定义在R上的几个函数,要我们找出其中的奇函数且是减函数的函数,着重考查了基本初等函数的单调性与奇偶性及其判断方法的知识,属于基础题.

练习册系列答案
相关题目
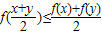 ,则称这个函数是下凸函数,下列函数
,则称这个函数是下凸函数,下列函数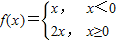
 ,则称这个函数是下凸函数,下列函数
,则称这个函数是下凸函数,下列函数