题目内容
8.已知函数f(x)=|1-x2|,在[0,1]上任取一数a,在[1,2]上任取一数b,则满足f(a)≤f(b)的概率为$\frac{6-π}{4}$.分析 由题意化简f(a)≤f(b)可得$\left\{\begin{array}{l}{a≤b}\\{{a}^{2}+{b}^{2}≥2}\end{array}\right.$,或$\left\{\begin{array}{l}{a≥b}\\{{a}^{2}+{b}^{2}≤2}\end{array}\right.$,而a∈[0,1],b∈[1,2],作出图形由几何概型可得.
解答 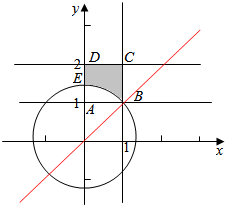 解:由题意可得f(a)≤f(b)即|1-a2|≤|1-b2|,
解:由题意可得f(a)≤f(b)即|1-a2|≤|1-b2|,
平方化简可得(a2-b2)(a2+b2-2)≤0
即$\left\{\begin{array}{l}{a≤b}\\{{a}^{2}+{b}^{2}≥2}\end{array}\right.$,或$\left\{\begin{array}{l}{a≥b}\\{{a}^{2}+{b}^{2}≤2}\end{array}\right.$,对应的区域如图阴影部分
而a∈[0,1],b∈[1,2],
图形AEB的面积s=$\frac{1}{8}$$π(\sqrt{2})^{2}$-$\frac{1}{2}$×1×1=$\frac{π-2}{4}$,
正方形ABCD的面积为1×1=1,
故可得所求概率为P=1-$\frac{π-2}{4}$=$\frac{6-π}{4}$;
故答案为:$\frac{6-π}{4}$.
点评 本题考查几何概型,得出f(a)≤f(b)的区域是解决问题的关键,属中档题.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案
相关题目
19.通过市场调查,得到某种产品的资金投入x万元与获得的利润y万元的数据,如表所示:
(1)根据上表提供的数据,用最小二乘法求线性回归方程;
(2)现投入资金10万元,求获得利润的估计值为多少万元?
(参考公式:$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_1}}-n\bar x\bar y}}{{\sum_{i=1}^n{{x_i}^2}-n{{\bar x}^2}}}$,$\hat a=\bar y-\hat b\bar x$)
| 资金投入x | 2 | 3 | 4 | 5 | 6 |
| 利润y | 2 | 3 | 5 | 6 | 9 |
(2)现投入资金10万元,求获得利润的估计值为多少万元?
(参考公式:$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_1}}-n\bar x\bar y}}{{\sum_{i=1}^n{{x_i}^2}-n{{\bar x}^2}}}$,$\hat a=\bar y-\hat b\bar x$)
3.函数y=ln$\sqrt{a{x^2}+2x-1}$的值域为R,则实数a的取值范围是( )
| A. | [0,+∞) | B. | [-1,0)∪(0,+∞) | C. | (-∞,-1) | D. | [-1,1) |
17.已知A是⊙O上一定点,在⊙O上其他位置任取一点B,连接A、B两点,所得弦的长度大于等于⊙O的半径的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{5}{6}$ | D. | $\frac{1}{2}$ |
 从某学校高三年级共800名男生中随机抽取50名测量身高,据测量被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160)、第二组[160,165);…第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第六组比第七组多1人,第一组和第八组人数相同.
从某学校高三年级共800名男生中随机抽取50名测量身高,据测量被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160)、第二组[160,165);…第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第六组比第七组多1人,第一组和第八组人数相同.