题目内容
已知偶函数f(x)=cosθsinx-sin(x-θ)+(tanθ-2)sinx-sinθ的最小值是0,求f(x)的最大值及此时x的集合.
解析：f(x)=cosθsinx-(sinxcosθ-cosxsinθ)+(tanθ-2)sinx-sinθ=sinθcosx+(tanθ-2)sinx-sinθ.
∵f(x)是偶函数,所以对任意x∈R,都有f(-x)=f(x)，
即sinθcos(-x)+(tanθ-2)sin(-x)-sinθ=sinθcosx+(tanθ-2)sinx-sinθ,
即(tanθ-2)sinx=0,
所以tanθ=2.
由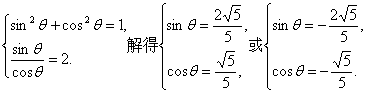
此时f(x)=sinθ(cosx-1).
当sinθ=
时,f(x)=
(cosx-1)，
最大值为0,不合题意舍去;
当sinθ=-
时,f(x)=-
(cosx-1)，最小值为0,当cosx=-1时,f(x)有最大值为
,
自变量x的集合为{x|x=2kπ+π,k∈Z}.
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
已知偶函数f(x+
)，当x∈(-
，
)时，f(x)=x
+sinx，设a=f（1），b=f（2），c=f（3），则（ ）
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 1 |
| 3 |
| A、a＜b＜c |
| B、b＜c＜a |
| C、c＜b＜a |
| D、c＜a＜b |