题目内容
(本小题12分)
过![]() 轴上动点
轴上动点![]() 引抛物线
引抛物线![]() 的两条切线
的两条切线![]() 、
、![]() ,
,![]() 、
、![]() 为切点.
为切点.
(1)若切线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() 和
和![]() ,求证:
,求证: ![]() 为定值,并求出定值;
为定值,并求出定值;
 (2)求证:直线
(2)求证:直线![]() 恒过定点,并求出定点坐标;
恒过定点,并求出定点坐标;
(3)当![]() 最小时,求
最小时,求![]() 的值.
的值.
解(1)![]() ,
,![]() ,
,
即![]() ,即
,即![]() ,
,
 同理
同理![]() ,所以
,所以![]() 。联立PQ的直线方程和抛物线方程可得:
。联立PQ的直线方程和抛物线方程可得:
![]() ,所以
,所以![]() ,所以
,所以![]()
![]() ……5分
……5分
(2)因为![]() ,所以直线
,所以直线![]() 恒过定点
恒过定点![]() …………9分
…………9分
(3)![]() ,所以
,所以![]()
![]() ,设
,设![]() ,所以
,所以![]()
![]() ,当且仅当
,当且仅当![]() 取等号,即
取等号,即![]() 。
。
因为![]()
![]()
因为![]()
所以![]()
![]() …………15分
…………15分

练习册系列答案
相关题目
 为
为 △ABC的外接圆,AB=AC,过点A的直线交⊙O于D,交BC延长线
△ABC的外接圆,AB=AC,过点A的直线交⊙O于D,交BC延长线 于F,DE是BD的延长线,连接CD。
于F,DE是BD的延长线,连接CD。
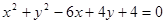 .
. 过点P且与圆心C的距离为1,求直线
过点P且与圆心C的距离为1,求直线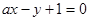 与圆C交于A、B两点,是否存在实数
与圆C交于A、B两点,是否存在实数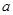 ,使得过点P(2,0)的直线
,使得过点P(2,0)的直线 垂直平
垂直平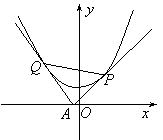 (2)求证:直线
(2)求证:直线