题目内容
平面直角坐标系中，O为坐标原点，已知两点A（1，2），B（-3，1）．若点P在线段AB上，且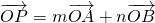
，则
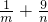有
- A.最小值-16
- B.最大值-16
- C.最大值16
- D.最小值16
D
分析：设P（x，y），由A（1，2），B（-3，1）可求得直线AB的方程为x-4y+7=0，再由点P在线段AB上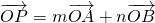，可求得m+n=1，代入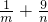，利用基本不等式即可．
解答：设P（x，y），由A（1，2），B（-3，1）得直线AB的斜率k=
，由点斜式可得直线AB的方程为x-4y+7=0，
又点P在线段AB上，
=m
+n
，
∴（x，y）=m（1，2）+n（-3，1），m＞0，n＞0
∴
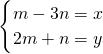，又x-4y+7=0，
∴（m-3n）-4（2m+n）+7=0，
∴m+n=1．又m＞0，n＞0，
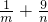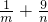∴=（）（m+n）=10+
+
≥10+6=16（当且仅当n=3m，即m=，n=时取到“=”）．
故选D．
点评：本题考查基本不等式，考查平面向量的基本定理及其意义，正确理解题意，得到m+n=1是关键，属于中档题．
分析：设P（x，y），由A（1，2），B（-3，1）可求得直线AB的方程为x-4y+7=0，再由点P在线段AB上，
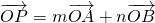可求得m+n=1，代入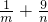，利用基本不等式即可．解答：设P（x，y），由A（1，2），B（-3，1）得直线AB的斜率k=
，由点斜式可得直线AB的方程为x-4y+7=0，又点P在线段AB上，
=m+n，∴（x，y）=m（1，2）+n（-3，1），m＞0，n＞0
∴
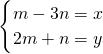，又x-4y+7=0，∴（m-3n）-4（2m+n）+7=0，
∴m+n=1．又m＞0，n＞0，
∴
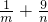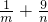=（）（m+n）=10++≥10+6=16（当且仅当n=3m，即m=，n=时取到“=”）．故选D．
点评：本题考查基本不等式，考查平面向量的基本定理及其意义，正确理解题意，得到m+n=1是关键，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
平面直角坐标系中，O为坐标原点，已知两点A（3，1）、B（-1，3），若点C满足
=α
+β
，其中α、β∈R，且α+β=1，则点C的轨迹方程为（ ）
| OC |
| OA |
| OB |
| A、3x+2y-11=0 |
| B、（x-1）2+（y-2）2=5 |
| C、2x-y=0 |
| D、x+2y-5=0 |
已知水平地面上有一篮球，在斜平行光线的照射下，其阴影为一椭圆（如图），在平面直角坐标系中，O为原点，设椭圆的方程为