Question

在直角坐标平面上，已知点A（0，2），B（0，1），D（t，0）（t＞0）．点M是线段AD上的动点，如果|AM|≤2|BM|恒成立，则正实数t的最小值是________．

Answer 1

分析：设M（x，y），由题意可得y=，代入距离公式可得x²+（y-2）²≤4[x²+（y-1）²]，消掉y可得（3t²+12）x²-16tx+4t²≥0恒成立，进而可得其△≤0，解此不等式可得t的范围，进而可得最小值．
解答：设M（x，y），则由A、M、D三点共线可得，整理可得y=，
由两点间的距离公式，结合|AM|≤2|BM|恒成立可得x²+（y-2）²≤4[x²+（y-1）²]，
整理可得3x²+3y²-4y≥0，代入y=化简可得（3t²+12）x²-16tx+4t²≥0恒成立，
∵3t²+12＞0，由二次函数的性质可得△=（-16t）²-4（3t²+12）•4t²≤0，
整理可得3t⁴-4t²≥0，即，解得t≥，或t≤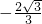（因为t＞0，故舍去）
故正实数t的最小值是：
故答案为：
点评：本题考查两点间的距离公式，涉及不等式的解法，属中档题．