题目内容
(2010•通州区一模)已知函数f(x)=2cos2x+2sinxcosx.
(I)求f(x)的最小正周期;
(II)若x∈[0,
],求f(x)的最大值与最小值的和.
(I)求f(x)的最小正周期;
(II)若x∈[0,
| π | 2 |
分析:(Ⅰ)先把f(x)=2cos2x+2sinxcosx等价转化为f(x)=cos2x+1+sin2x,从而得到f(x)=
sin(2x+
)+1,由此能求出函数f(x)的最小正周期.
(Ⅱ)当x∈[0,
]时,2x+
∈[
,
],由此能求出 f(x)的最大值与最小值的和.
| 2 |
| π |
| 4 |
(Ⅱ)当x∈[0,
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
解答:解:(Ⅰ)f(x)=2cos2x+2sinxcosx
=2cos2x-1+2sinxcosx+1
=cos2x+1+sin2x
=
sin(2x+
)+1,
∴函数f(x)的最小正周期 T=
=π.
(Ⅱ)当x∈[0,
]时,2x+
∈[
,
],
当2x+
=
,即x=
时,
f(x)取得最大值f(
) =
+1;
当2x+
=
,即x=
时,
f(x)取得最小值f(
) =
(-
) +1=0.
∴当x∈[0,
]时,
f(x)最大值与最小值的和为f(
) +f(
) =
+1.
=2cos2x-1+2sinxcosx+1
=cos2x+1+sin2x
=
| 2 |
| π |
| 4 |
∴函数f(x)的最小正周期 T=
| 2π |
| 2 |
(Ⅱ)当x∈[0,
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
当2x+
| π |
| 4 |
| π |
| 2 |
| π |
| 8 |
f(x)取得最大值f(
| π |
| 8 |
| 2 |
当2x+
| π |
| 4 |
| 5π |
| 4 |
| π |
| 2 |
f(x)取得最小值f(
| π |
| 2 |
| 2 |
| ||
| 2 |
∴当x∈[0,
| π |
| 2 |
f(x)最大值与最小值的和为f(
| π |
| 8 |
| π |
| 2 |
| 2 |
点评:本题考查三角函数的综合运用,解题时要认真审题,注意二倍角公式和一角一函数及三角函数性质的灵活运用,易错点是三角函数符号的选取.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
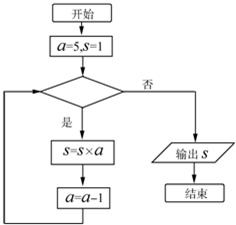 (2010•通州区一模)执行图所示的程序,输出的结果为20,则判断框中应填入的条件为( )
(2010•通州区一模)执行图所示的程序,输出的结果为20,则判断框中应填入的条件为( )
 (2010•通州区一模)设不等式组
(2010•通州区一模)设不等式组