题目内容
【题目】已知函数
（
）.
（1）若曲线
在点
处的切线方程为
，求a的值；
（2）若
是函数
的极值点，且
，求证：
.
【答案】（1）
（2）见解析
【解析】
（1）求出切线方程
，与
对比系数即可；
（2）
，令
，通过讨论知
，且
，从而
，再由
确定出
的范围即可获证.
解：（1）由题意知，
的定义域为
，
，
则
，
又
，
所以曲线
在点
处的切线方程为
，
即，
所以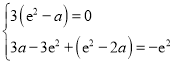
，解得.
（2）由（1）得，，显然
.
令，
，
当
时，
，在
上单调递增，无极值，不符合题意；
当时，
，所以
在上单调递增
取b满足
，则
，
，
所以
.
又
，所以存在
，使得
，此时.
又当
时，
，
，单调递减，
当
时，
，，单调递增，
所以为函数的极小值点，且.
令
，则
，所以
在上单调递减，
又
，
，所以
，∴ 
；
令
，则
.
所以当时，
单调递增，所以
，所以
，
所以
.
练习册系列答案
相关题目
【题目】某学校为了解该校高三年级学生数学科学习情况，对一模考试数学成绩进行分析，从中抽取了
名学生的成绩作为样本进行统计，该校全体学生的成绩均在
，按照
，
，
，
，
，
，
，
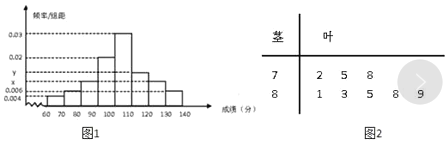
的分组作出频率分布直方图如图（1）所示，样本中分数在
内的所有数据的茎叶图如图（2）所示．根据上级统计划出预录分数线，有下列分数与可能被录取院校层次对照表为表（3）．
分数 |
|
|
|
可能被录取院校层次 | 专科 | 本科 | 重本 |
图（3）
（1）求和频率分布直方图中的
，
的值；
（2）根据样本估计总体的思想，以事件发生的频率作为概率，若在该校高三年级学生中任取3人，求至少有一人是可能录取为重本层次院校的概率；
（3）在选取的样本中，从可能录取为重本和专科两个层次的学生中随机抽取3名学生进行调研，用表示所抽取的3名学生中为重本的人数，求随机变量
的分布列和数学期望．
