题目内容
已知函数f(x)=|x-3|-2,g(x)=-|x+1|+4,
(1)若函数f(x)的值不大于1,求x的取值范围;
(2)若不等式f(x)-g(x)≥m+1的解集为R,求实数m的取值范围.
(1)若函数f(x)的值不大于1,求x的取值范围;
(2)若不等式f(x)-g(x)≥m+1的解集为R,求实数m的取值范围.
解:(1)由题意得f(x)≤1,即|x-3|-2≤1,
解得0≤x≤6,
所以x的取值范围是[0,6];
(2)f(x)-g(x)=|x-3|+|x+1|-6,
对于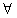 x∈R,由绝对值不等式的性质得
x∈R,由绝对值不等式的性质得
f(x)-g(x)=|x-3|+|x+1|-6=|3-x|+|x+1|-6≥|(3-x)+(x+1)|-6=4-6=-2,
于是有m+1≤-2,得m≤-3,
即m的取值范围是(-∞,-3]。
解得0≤x≤6,
所以x的取值范围是[0,6];
(2)f(x)-g(x)=|x-3|+|x+1|-6,
对于
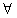 x∈R,由绝对值不等式的性质得
x∈R,由绝对值不等式的性质得f(x)-g(x)=|x-3|+|x+1|-6=|3-x|+|x+1|-6≥|(3-x)+(x+1)|-6=4-6=-2,
于是有m+1≤-2,得m≤-3,
即m的取值范围是(-∞,-3]。

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|