题目内容
已知点A(3,0),B(0,3),C(cosα,sinα)
(1)若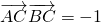 ,求sin2α的值;
,求sin2α的值;
(2)若 ,其中O是原点,且α∈(0,π),求
,其中O是原点,且α∈(0,π),求 与
与 的夹角.
的夹角.
解:(1)由题意可得  ,
,
(cosα-3)cosα+sinα(sinα-3)=-1,化简得: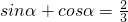 ,上式平方,解得:
,上式平方,解得: .
.
(2)由 ,∴
,∴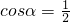 ,∵α∈(0,π),∴
,∵α∈(0,π),∴ ,
,
∴ ,∴
,∴ ,
,
∴ .
.
分析:(1)求出 和
和  的坐标,根据
的坐标,根据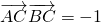 可得 sinα+cosα=
可得 sinα+cosα= ,平方可得
,平方可得 .
.
(2)由 ,可得
,可得 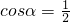 ,由α∈(0,π),求得
,由α∈(0,π),求得  ,从而得到C的坐标,根据
,从而得到C的坐标,根据
 ,运算求得结果.
,运算求得结果.
点评:本题考查两个向量的数量积的定义,两个向量的数量积公式,根据三角函数的值求角,是一道中档题.
 ,
,(cosα-3)cosα+sinα(sinα-3)=-1,化简得:
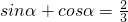 ,上式平方,解得:
,上式平方,解得: .
.(2)由
 ,∴
,∴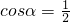 ,∵α∈(0,π),∴
,∵α∈(0,π),∴ ,
,∴
 ,∴
,∴ ,
,∴
 .
.分析:(1)求出
 和
和  的坐标,根据
的坐标,根据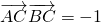 可得 sinα+cosα=
可得 sinα+cosα= ,平方可得
,平方可得 .
.(2)由
 ,可得
,可得 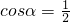 ,由α∈(0,π),求得
,由α∈(0,π),求得  ,从而得到C的坐标,根据
,从而得到C的坐标,根据 ,运算求得结果.
,运算求得结果.点评:本题考查两个向量的数量积的定义,两个向量的数量积公式,根据三角函数的值求角,是一道中档题.

练习册系列答案
相关题目
已知点A(3,0),B(-
,1),C(cosa,sina),O(0,0),若|
+
|=
,a∈(0,π),则
与
的夹角为( )
| 3 |
| OA |
| OC |
| 13 |
| OB |
| OC |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,已知点A(
如图,已知点A(