题目内容
求函数y=sin4x+
解:y=sin4x+![]() sinxcosx-cos4x
sinxcosx-cos4x
=(sin2x-cos2x)(sin2x+cos2x)+![]() sin2x
sin2x
=-cos2x+![]() sin2x
sin2x
=2(![]() sin2x-
sin2x-![]() cos2x)
cos2x)
=2sin(2x-![]() ),
),
则T=![]() =
=![]() =π,y最小=-2.
=π,y最小=-2.
由于y=sinx的增区间为2kπ![]() ≤x≤2kπ+
≤x≤2kπ+![]() ,
,
故y=2sin(2x-![]() )的增区间为2kπ
)的增区间为2kπ![]() ≤2x
≤2x![]() ≤2kπ+
≤2kπ+![]()
![]() 2kπ-
2kπ-![]() ≤2x≤2kπ+
≤2x≤2kπ+![]()
![]() kπ-
kπ-![]() ≤x≤kπ+
≤x≤kπ+![]() .
.
当k=0时,![]() ≤x≤
≤x≤![]() ,
,
当k=1时,![]() ≤x≤
≤x≤![]() .
.
由于x∈[0,π],
所以单调增区间为[0,![]() ]与[
]与[![]() ,π].
,π].

练习册系列答案
相关题目
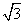 sinxcosx-cos4x的最小正周期和最小值;并写出该函数在[0,π]上的单调递增区间。
sinxcosx-cos4x的最小正周期和最小值;并写出该函数在[0,π]上的单调递增区间。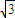 sinxcosx-cos4x的最小正周期和最小值;并写出该函数在[0,π]上的单调递增区间.
sinxcosx-cos4x的最小正周期和最小值;并写出该函数在[0,π]上的单调递增区间.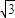 sinxcosx-cos4x的最小正周期和最小值;并写出该函数在[0,π]上的单调递增区间.
sinxcosx-cos4x的最小正周期和最小值;并写出该函数在[0,π]上的单调递增区间.