题目内容
已知:O是△ABC所在平面上的一点且满足:
+
(
-
)+
(
-
)=
,则点O在( )
| OA |
| sinA |
| sinA+sinB |
| OB |
| OA |
| sinB |
| sinB+sinA |
| OC |
| OA |
| 0 |
| A、AB边上 | B、AC边上 |
| C、BC边上 | D、△ABC内心 |
分析:先对条件
+
(
-
)+
(
-
)=
进行化简整理可得sinA
=-sinB
,根据共线定理可知
与
共线,即点O在BC边上从而得到结论.
| OA |
| sinA |
| sinA+sinB |
| OB |
| OA |
| sinB |
| sinB+sinA |
| OC |
| OA |
| 0 |
| OB |
| OC |
| OB |
| OC |
解答:解:∵
+
(
-
)+
(
-
)=
,
∴(sinA+sinB)
+sinA•
+sinB•
=
即sinA
+sinB
=
sinA
=-sinB
∴
与
共线,即点O在BC边上
故选C.
| OA |
| sinA |
| sinA+sinB |
| OB |
| OA |
| sinB |
| sinB+sinA |
| OC |
| OA |
| 0 |
∴(sinA+sinB)
| OA |
| AB |
| AC |
| 0 |
即sinA
| OB |
| OC |
| 0 |
sinA
| OB |
| OC |
∴
| OB |
| OC |
故选C.
点评:本题主要考查向量的共线定理.要证明三点共线时一般转化为证明向量的共线问题.

练习册系列答案
相关题目
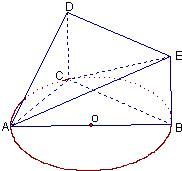 如图,△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行
如图,△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行 (2012•九江一模)已知点G是△ABC的外心,
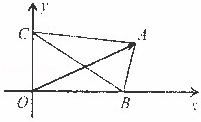
(2012•九江一模)已知点G是△ABC的外心, 平面ABC ,
平面ABC , ,已知AE与平面ABC所成的角为
,已知AE与平面ABC所成的角为 ,且
,且 .
. ;
; ,
, 表示三棱锥A-CBE的体积,求
表示三棱锥A-CBE的体积,求
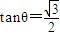 .
.