Question

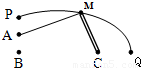
如图，A村在B地正北3 km处，C村在B地正东4 km处，已知弧形公路PQ上任一点到B、C两点的距离之和为8 km，现要在公路旁建造一个交电房M分别向A村、C村送电，但C村有一村办工厂用电需用专用线路，不得与民用混线用电，因此向C村送电要架两条线路，分别给村民和工厂送电，要使用电线最短，电房M应建在A村的什么方位，并求出M到A村的距离．

Answer 1

答案：
解析：

解：以直线BC为x轴，线段BC的中垂线为y轴，建立如图所示的直角坐标系，由题意，得|MB|＋|MC|＝8＞4＝|BC|， 　　∴点M在以B、C为焦点，长轴长为8 km的椭圆上． 　　由2a＝8，2c＝4，得a＝4，c＝2．∴b＝2． 　　∴椭圆方程为 　　其右准线l：x＝8，离心率e＝．作MN⊥l于N，则，|MN|＝2|MC|． 　　作AE⊥l于E交椭圆于(介于A、E之间)． 　　∴|MA|＋2|MC|＝|MA|＋|MN|≥|A|＋|E|＝|AE|＝8－(－2)＝10． 　　∴(|MA|＋2|MC|)min＝10，此时M与的点重合． 　　由解得()， 　　即M()． 　　此时|AM|＝2＋2＝2(＋1)， 　　即要使用电线最短，电房M应建在A的正东方向，距A村2(＋1)km处．