题目内容
设各项均为正数的数列{an}满足a1=2,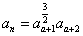 (n∈N*),
(n∈N*),
(Ⅰ)若a2=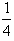 ,求a3,a4,并猜想a2cos的值(不需证明);
,求a3,a4,并猜想a2cos的值(不需证明);
(Ⅱ)记bn=a3a2…an(n∈N*),若bn≥2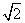 对n≥2恒成立,求a2的值及数列{bn}的通项公式。
对n≥2恒成立,求a2的值及数列{bn}的通项公式。
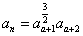 (n∈N*),
(n∈N*),(Ⅰ)若a2=
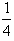 ,求a3,a4,并猜想a2cos的值(不需证明);
,求a3,a4,并猜想a2cos的值(不需证明);(Ⅱ)记bn=a3a2…an(n∈N*),若bn≥2
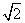 对n≥2恒成立,求a2的值及数列{bn}的通项公式。
对n≥2恒成立,求a2的值及数列{bn}的通项公式。 解:(Ⅰ)因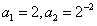 ,
,
故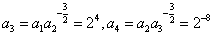 ,
,
由此有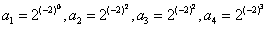 ,
,
故猜想{an}的通项为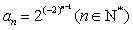 。
。
(Ⅱ)令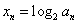 ,Sn表示xn的前n项和,则
,Sn表示xn的前n项和,则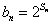 ,
,
由题设知x1=1且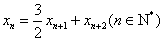 ,①
,①
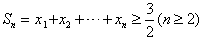 ,②
,②
因②式对n=2成立,有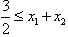 ,
,
又x1=1得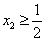 ,③
,③
下用反证法证明: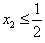 ,
,
假设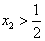 ,
,
由①得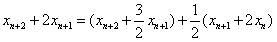 ,
,
因此数列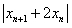 是首项为
是首项为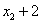 ,公比为
,公比为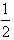 的等比数列,
的等比数列,
故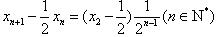 ,④
,④
又由①知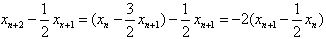 ,
,
因此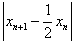 是首项为
是首项为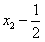 ,公比为-2的等比数列,
,公比为-2的等比数列,
所以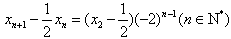 ,⑤
,⑤
由④-⑤得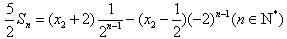 ,⑥
,⑥
对n求和得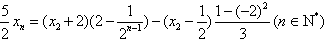 ,⑦
,⑦
由题设知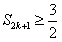 ,且由反证假设
,且由反证假设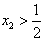 ,
,
有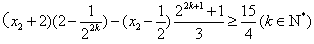 ,
,
从而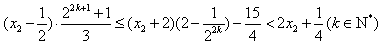 ,
,
即不等式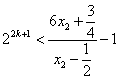 对k∈N*恒成立,但这是不可能的,矛盾;
对k∈N*恒成立,但这是不可能的,矛盾;
因此x2≤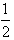 ,结合③式知x2=
,结合③式知x2=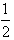 ,
,
因此a2=2*2=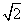 ,
,
将x2=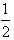 代入⑦式得Sn=2-
代入⑦式得Sn=2-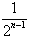 (n∈N*),
(n∈N*),
所以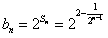 (n∈N*)。
(n∈N*)。
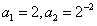 ,
,故
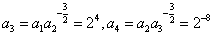 ,
,由此有
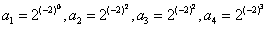 ,
,故猜想{an}的通项为
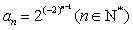 。
。(Ⅱ)令
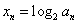 ,Sn表示xn的前n项和,则
,Sn表示xn的前n项和,则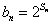 ,
,由题设知x1=1且
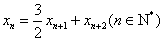 ,①
,① 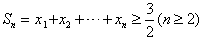 ,②
,② 因②式对n=2成立,有
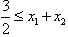 ,
,又x1=1得
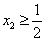 ,③
,③下用反证法证明:
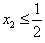 ,
,假设
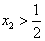 ,
,由①得
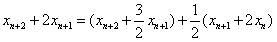 ,
,因此数列
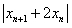 是首项为
是首项为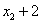 ,公比为
,公比为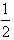 的等比数列,
的等比数列,故
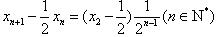 ,④
,④ 又由①知
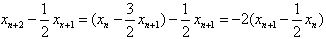 ,
,因此
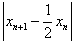 是首项为
是首项为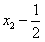 ,公比为-2的等比数列,
,公比为-2的等比数列,所以
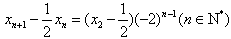 ,⑤
,⑤ 由④-⑤得
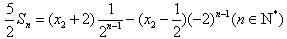 ,⑥
,⑥ 对n求和得
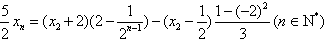 ,⑦
,⑦ 由题设知
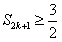 ,且由反证假设
,且由反证假设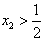 ,
,有
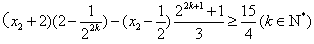 ,
,从而
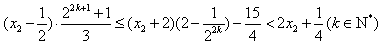 ,
,即不等式
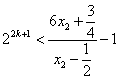 对k∈N*恒成立,但这是不可能的,矛盾;
对k∈N*恒成立,但这是不可能的,矛盾;因此x2≤
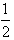 ,结合③式知x2=
,结合③式知x2=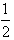 ,
,因此a2=2*2=
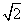 ,
,将x2=
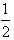 代入⑦式得Sn=2-
代入⑦式得Sn=2-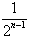 (n∈N*),
(n∈N*),所以
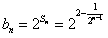 (n∈N*)。
(n∈N*)。
练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目