��Ŀ����
����������յĶ��壺�����ڶ�����D�ڵ�����һ���Ա���x0�����к���ֵf��x0����D����ƺ���y=f��x����D�Ϸ�գ�
��1����������D1=��0��1�����ж����к�������Щ��D1�Ϸ�գ�д���������̣���f1��x��=2x-1��f2��x��=-
x2-
x+1��f3��x��=2x-1��
��2����������D2=��1��2�����Ƿ����ʵ��a��ʹ�ú���f��x��=
��D2�Ϸ�գ������ڣ����a��ֵ��������֤�����������ڣ���˵�����ɣ�
��1����������D1=��0��1�����ж����к�������Щ��D1�Ϸ�գ�д���������̣���f1��x��=2x-1��f2��x��=-
| 1 |
| 2 |
| 1 |
| 2 |
��2����������D2=��1��2�����Ƿ����ʵ��a��ʹ�ú���f��x��=
| 5x-a |
| x+2 |
��������1�����ݶ�������ú����Ķ����������¶��壬���ɵõ����ۣ�
��2���������ۣ�ȷ�������ĵ����ԣ���������ʽ�飬����a��ֵ��
��2���������ۣ�ȷ�������ĵ����ԣ���������ʽ�飬����a��ֵ��
����⣺��1�����ڶ�����D�ڵ�����һ���Ա���x0�����к���ֵf1��x0���ʣ�-1��1��∉D1��
�ʺ���f1��x��=2x-1��D1�ϲ���գ�
ͬ����f2��x��=-
x2-
x+1=-
(x+
)2+
�ʣ�0��1����f3��x��=2x-1�ʣ�0��1��������D1�Ϸ�գ�
��2��f��x��=
���Գ�����Ϊ��-2��5��
��a+10��0ʱ������f��x��=
��D2��Ϊ��������ֻ��
����a=2
��a+10��0ʱ������f��x��=
��D2��Ϊ��������ֻ��
����a��∅
���ϣ�����a��ֵ����2��
�ʺ���f1��x��=2x-1��D1�ϲ���գ�
ͬ����f2��x��=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 8 |
��2��f��x��=
| 5x-a |
| x+2 |
��a+10��0ʱ������f��x��=
| 5x-a |
| x+2 |
|
��a+10��0ʱ������f��x��=
| 5x-a |
| x+2 |
|
���ϣ�����a��ֵ����2��
�������������¶��庯��Ϊ���壬�����¶��壬����ѧ���ļ����������ؼ��Ƕ��¶�������⣬��һ�����Ѷȣ�

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
 �����к���ֵ
�����к���ֵ ,��ƺ���y=f��x���� D�Ϸ�ա�
,��ƺ���y=f��x���� D�Ϸ�ա� �ж����к�������Щ��
�ж����к�������Щ�� �Ϸ�գ��������������̣�
�Ϸ�գ��������������̣�
 �Ƿ����ʵ��
�Ƿ����ʵ�� ��ʹ����
��ʹ���� ��
�� �Ϸ�գ������ڣ����
�Ϸ�գ������ڣ���� -
- +1��f3��x��=2x-1��
+1��f3��x��=2x-1��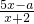 ��D2�Ϸ�գ������ڣ����a��ֵ��������֤�����������ڣ���˵�����ɣ�
��D2�Ϸ�գ������ڣ����a��ֵ��������֤�����������ڣ���˵�����ɣ�