题目内容
设 ,则
,则
A. | B. | C. | D. |
D
解析试题分析:因为, ,即
,即 ,
,
所以,两边平方得, ,选D。
,选D。
考点:本题主要考查两角和差的三角函数,倍角公式。
点评:简单题,涉及正弦函数与余弦函数的“和”“积”互化问题,往往通过平方实现。

练习册系列答案
相关题目
函数 的最小正周期为( )
的最小正周期为( )
A.4 | B.2 | C. | D. |
若 ,则
,则 ( )
( )
A. | B. | C. | D. |
在 中,内角
中,内角 所对的边分别是
所对的边分别是 . 若
. 若 ,
, ,
, ,则
,则
| A.2 | B.3 | C.4 | D.6 |
函数 是( )
是( )
A.周期为 的奇函数 的奇函数 | B.周期为4 的偶函数 的偶函数 |
C.周期为 的偶函数 的偶函数 | D.周期为 的奇函数 的奇函数 |
已知 ,且
,且 ,则
,则 =( )
=( )
| A.-1 | B. | C. | D. |
观察等式


由此得出以下推广命题不正确的是
A. |
B. |
C. |
D. |
化简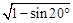 的结果是( )
的结果是( )
A. | B. | C. | D. |
定义运算: ,则
,则 的值是( )
的值是( )
A. | B. | C. | D. |