题目内容
已知直线l与函数f(x)=lnx的图象相切于点(1,0),且l与函数g(x)=
x2+mx+
(m<0)的图象也相切.
(Ⅰ)求直线l的方程及m的值;
(Ⅱ)若h(x)=f(x+1)-g′(x)(其中g′(x)是g(x)的导函数),求函数h(x)的最大值;
(Ⅲ)当0<a<1时,求证:f(1+a)-f(2)<
.
| 1 |
| 2 |
| 7 |
| 2 |
(Ⅰ)求直线l的方程及m的值;
(Ⅱ)若h(x)=f(x+1)-g′(x)(其中g′(x)是g(x)的导函数),求函数h(x)的最大值;
(Ⅲ)当0<a<1时,求证:f(1+a)-f(2)<
| a-1 |
| 2 |
(Ⅰ)∵f′(x)=
,直线l是函数f(x)=lnx的图象在点(1,0)处的切线,
∴其斜率为k=f′(1)=1
∴直线l的方程为y=x-1.
又因为直线l与g(x)的图象相切
∴
?
x2+(m-1)x+
=0,
得△=(m-1)2-9=0?m=-2(m=4不合题意,舍去)
(Ⅱ)由(Ⅰ)知,g(x)=
x2-2x+
∴h(x)=f(x+1)-g′(x)=ln(x+1)-x+2(x>-1),
∴h′(x)=
-1=
.(x>-1)
当-1<x<0时,h′(x)>0;当x>0时,h′(x)<0.
于是,h(x)在(-1,0)上单调递增,在(0,+∞)上单调递减.
所以,当x=0时,h(x)取得最大值h(0)=2;
(Ⅲ)由(Ⅱ)知:当-1<x<0时,h(x)<2,即ln(1+x)<x,
当0<a<1时,-1<
<0
∴f(1+a)-f(2)=ln
=ln(1+
)<
.
| 1 |
| x |
∴其斜率为k=f′(1)=1
∴直线l的方程为y=x-1.
又因为直线l与g(x)的图象相切
∴
|
| 1 |
| 2 |
| 9 |
| 2 |
得△=(m-1)2-9=0?m=-2(m=4不合题意,舍去)
(Ⅱ)由(Ⅰ)知,g(x)=
| 1 |
| 2 |
| 7 |
| 2 |
∴h(x)=f(x+1)-g′(x)=ln(x+1)-x+2(x>-1),
∴h′(x)=
| 1 |
| x+1 |
| -x |
| x+1 |
当-1<x<0时,h′(x)>0;当x>0时,h′(x)<0.
于是,h(x)在(-1,0)上单调递增,在(0,+∞)上单调递减.
所以,当x=0时,h(x)取得最大值h(0)=2;
(Ⅲ)由(Ⅱ)知:当-1<x<0时,h(x)<2,即ln(1+x)<x,
当0<a<1时,-1<
| a-1 |
| 2 |
∴f(1+a)-f(2)=ln
| 1+a |
| 2 |
| a-1 |
| 2 |
| a-1 |
| 2 |

练习册系列答案
相关题目
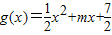 (m<0)的图象也相切.
(m<0)的图象也相切.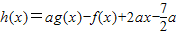 ,若
,若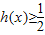 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.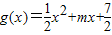 (m<0)的图象也相切.
(m<0)的图象也相切.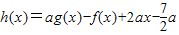 ,若
,若 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.