题目内容
设椭圆的方程为![]() ,线段PQ是过左焦点F且不与x轴垂直的焦点弦.若在左准线上存在点R,使△PQR为正三角形,求椭圆的离心率e的取值范围,并用e表示直线PQ的斜率.
,线段PQ是过左焦点F且不与x轴垂直的焦点弦.若在左准线上存在点R,使△PQR为正三角形,求椭圆的离心率e的取值范围,并用e表示直线PQ的斜率.
答案:
解析:
解析:
|
■少图 解:如图,设线段 过点 假设存在点 所以, 于是, 若 当 若 又 |

练习册系列答案
相关题目
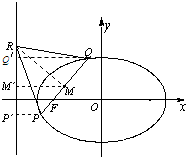 设椭圆的方程为
设椭圆的方程为