题目内容
△ABC中,角A、B、C所对应的边分别为a、b、c,若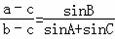
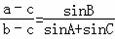
(1)求角A;
(2)若函数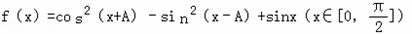 ,求函数f(x)的取值范围.
,求函数f(x)的取值范围.
(2)若函数
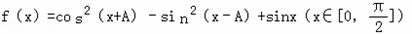 ,求函数f(x)的取值范围.
,求函数f(x)的取值范围.解:(1)由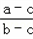 =
=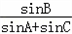 ,得
,得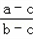 =
=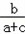 ,
,
即a2=b2+c2﹣bc,即bc=b2+c2﹣a2,

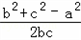 =
= ,
,
又根据余弦定理得到cosA= ,
,
 0<A<
0<A<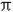 ,
,
 A=
A=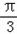 ;
;
(2)f(x)=cos2(x+A)﹣sin2(x﹣A)+sinx
=cos2(x+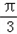 )﹣sin2(x﹣
)﹣sin2(x﹣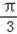 )+sinx
)+sinx
=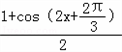 ﹣
﹣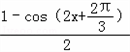 +sinx
+sinx
=sin2x+sinx﹣ =(sinx+
=(sinx+ )2﹣
)2﹣ ,
,
 x
x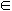 [0,
[0,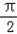 ],
],
 sinx
sinx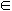 [0,1],f(x)的取值范围[﹣
[0,1],f(x)的取值范围[﹣ ,
, ]
]
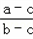 =
=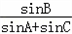 ,得
,得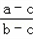 =
=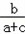 ,
,即a2=b2+c2﹣bc,即bc=b2+c2﹣a2,

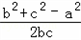 =
= ,
,又根据余弦定理得到cosA=
 ,
, 0<A<
0<A<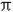 ,
, A=
A=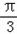 ;
;(2)f(x)=cos2(x+A)﹣sin2(x﹣A)+sinx
=cos2(x+
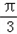 )﹣sin2(x﹣
)﹣sin2(x﹣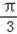 )+sinx
)+sinx=
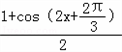 ﹣
﹣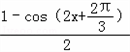 +sinx
+sinx=sin2x+sinx﹣
 =(sinx+
=(sinx+ )2﹣
)2﹣ ,
, x
x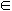 [0,
[0,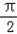 ],
], sinx
sinx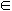 [0,1],f(x)的取值范围[﹣
[0,1],f(x)的取值范围[﹣ ,
, ]
]
练习册系列答案
相关题目