题目内容

已知直线l的参数方程为数学公式（参数t∈R），圆C的参数方程为数学公式（参数θ∈[0，2π]），则直线l被圆C所截得的弦长为 ________．


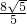
分析：把参数方程中的参数消去可分别求得直线和圆的方程，进而可知圆的圆心和半径，利用点到直线的距离求得圆心到直线的距离，进而利用勾股定理求得弦长．
解答：依题意可知直线l的方程为2x+y-6=0，圆的方程为（x-2）2+y2=4
∴圆心为（2，0），半径为2，
∴圆心到直线的距离d==
则弦长为2=
故答案为：
点评：本题主要考查了直线与圆相交的性质，直线和圆的参数方程．解题的过程中主要是通过消去参数，把参数方程转化为一般的方程来解决．
练习册系列答案
相关题目
C选修4-4：坐标系与参数方程已知直线l的参数方程：
x=2t
y=1+4t
（t为参数），曲线C的极坐标方程：ρ=2
2
sin（θ+
π
4
），求直线l被曲线C截得的弦长．
极坐标与参数方程：
已知直线l的参数方程是：
x=2t
y=1+4t
（t为参数），圆C的极坐标方程是：ρ=2
2
sin（θ+
π
4
），试判断直线l与圆C的位置关系．
已知直线l的参数方程为
x=
1
2
t
y=2+
3
2
t
（t为参数），曲线C的极坐标方程是ρ=
sinθ
1-sin2θ
以极点为原点，极轴为x轴正方向建立直角坐标系，点M（0，2），直线l与曲线C交于A，B两点．
（1）写出直线l的普通方程与曲线C的直角坐标方程；
（2）线段MA，MB长度分别记|MA|，|MB|，求|MA|•|MB|的值．
（坐标系与参数方程选做题） 已知直线l的参数方程为
x=
2
2
t
y=1+
2
2
t
（t为参数），圆C的参数方程为
x=cosθ+2
y=sinθ
（θ为参数），则圆心C到直线l的距离为
3
2
2
．
3
2
2
．
．
（2013•香洲区模拟）已知直线L的参数方程为：
x=t
y=a+
3
t
（t为参数），圆C的参数方程为：
x=sinθ
y=cosθ+1
（θ为参数）．若直线L与圆C有公共点，则常数a的取值范围是
[-1，3]
[-1，3]
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网