题目内容
(本小题满分12分)
已知函数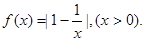
(1)是否存在实数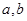
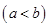 ,使得函数
,使得函数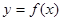 的定义域、值域都是
的定义域、值域都是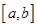 ,若存在,则求出
,若存在,则求出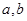 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
(2)若存在实数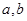
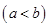 ,使得函数
,使得函数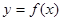 的定义域为
的定义域为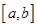 时,值域为
时,值域为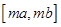 (
(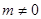 ),求
),求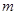 的取值范围.
的取值范围.
已知函数
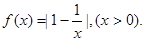
(1)是否存在实数
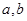
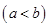 ,使得函数
,使得函数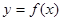 的定义域、值域都是
的定义域、值域都是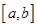 ,若存在,则求出
,若存在,则求出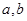 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.(2)若存在实数
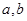
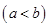 ,使得函数
,使得函数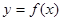 的定义域为
的定义域为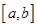 时,值域为
时,值域为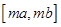 (
(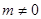 ),求
),求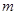 的取值范围.
的取值范围.(1) 不存在适合条件的实数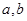 (2)
(2) 
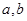 (2)
(2) 
试题分析:解:(1)若存在满足条件的实数
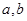 ,使得函数
,使得函数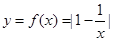 的定义域、值域都是
的定义域、值域都是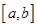 ,则
,则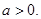 由题意知
由题意知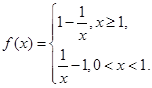

① 当
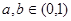 时,
时,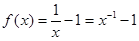 在
在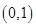 上为减函数.故
上为减函数.故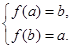 即
即 解得
解得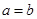 ,故此时不存在适合条件的实数
,故此时不存在适合条件的实数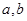
②当
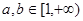 时,
时,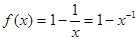 在
在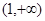 上是增函数. 故
上是增函数. 故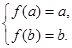 即
即 ,此时
,此时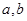 是方程
是方程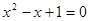 的根,此方程无实根.故此时不存在适合条件的实数
的根,此方程无实根.故此时不存在适合条件的实数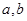
③当
 时, 由于
时, 由于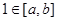 ,而
,而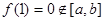 ,故此时不存在适合条件的实数
,故此时不存在适合条件的实数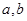 ,综上可知,不存在适合条件的实数
,综上可知,不存在适合条件的实数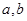 .
. (2)若存在实数
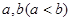 ,使得函数
,使得函数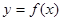 的定义域为
的定义域为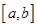 时,值域为
时,值域为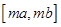
则
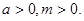
①当
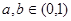 时,由于
时,由于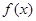 在
在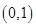 上是减函数,值域为
上是减函数,值域为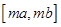 ,
, 即
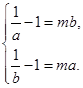 此时
此时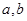 异号,不合题意.所以
异号,不合题意.所以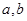 不存在.
不存在.②当
 或
或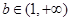 时,由(1)知0在值域内,值域不可能是
时,由(1)知0在值域内,值域不可能是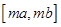 ,所以
,所以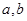 不存在,故只有
不存在,故只有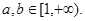
又因为
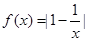 在
在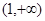 上是增函数,
上是增函数,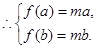 即
即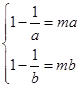
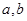 是方程
是方程 的两个根,即关于
的两个根,即关于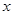 的方程
的方程 有两个大于
有两个大于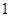 的实根.设这两个根为
的实根.设这两个根为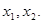 则
则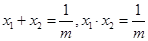
所以
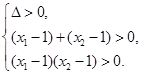 即
即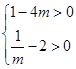 解得
解得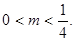
故
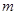 的取值范围是
的取值范围是
点评:解决函数的定义域和值域的问题,主要是分析函数的单调性,对于含有绝对值的 函数实际就是分段函数,要分别考虑求解其值域,同时要注意分段函数的值域等于各段函数值域的并集,定义域也是各段定义域的并集,属于难度试题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
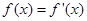 的实数根
的实数根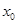 叫做函数
叫做函数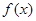 的“新驻点”,若函数
的“新驻点”,若函数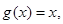
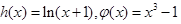 的“新驻点”分别为
的“新驻点”分别为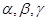 ,则
,则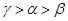
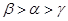
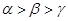
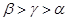
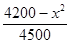 ,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%).
,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%).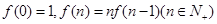 ,则
,则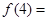
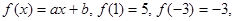 求
求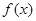
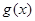 分别由下表给出:
分别由下表给出:
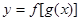 ,并画出函数
,并画出函数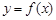 满足:①
满足:①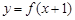 是偶函数;②在区间
是偶函数;②在区间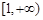 上是增函数.若
上是增函数.若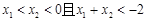 ,则
,则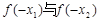 的大小关系是( )
的大小关系是( )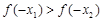
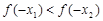
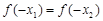
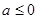 ,函数
,函数 .
. 在
在 上的奇偶性;
上的奇偶性;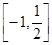 上的最大值。
上的最大值。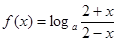 (
(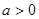 且
且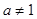 ).
).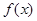 的定义域;
的定义域;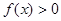 的
的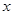 取值范围.
取值范围.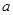 吨,计划正式运营后的第一年进油量为已储油量的
吨,计划正式运营后的第一年进油量为已储油量的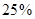 ,以后每年的进油量为上一年年底储油量的
,以后每年的进油量为上一年年底储油量的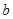 吨,设
吨,设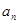 为正式运营第n年年底的储油量。(其中
为正式运营第n年年底的储油量。(其中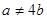 )
)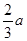 吨,如果
吨,如果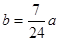 吨,该油库能否长期按计划运营?如果可以请加以证明;如果不行请求出最多可以运营几年。(取
吨,该油库能否长期按计划运营?如果可以请加以证明;如果不行请求出最多可以运营几年。(取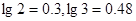 )
)