题目内容
对n∈N?不等式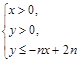
所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列(x1,y1),(x2,y2),?,(xn,yn),
求xn,yn;
(2)数列{an}满足a1=x1,且n≥2时an=yn2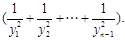
证明:当n≥2时,
;
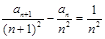(3)在(2)的条件下,试比较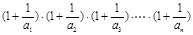
与4的大小关系.
（1）
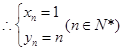
（2）运用整体的思想，作差法来得到化简证明。
（3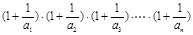）<4
解析试题分析：解：（1）当n=1时，（x1,y1）=(1,1)
n=2时，（x2,y2）="(1,2)" （x3,y3）=(1,3)
n=3时，（x4,y4）=(1,4)
n时 （xn,yn）=(1,n)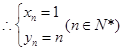
（2）由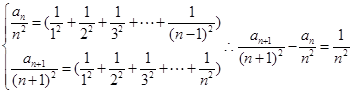
（3）当n=1时，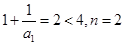
时，
成立
由（2）知当n≥3时，
即
=
=
=
=
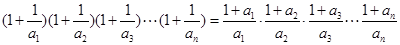
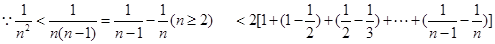
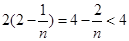得证
考点：本试题主要是考查了数列与不等式的综合运用。
点评：对于数列与不等式结合的证明试题，是个难点，一般要用到放缩法来证明，需要同学们注意积累相关的放缩的方法。
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
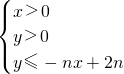所表示的平面区域为Dn，把Dn内的整点（横坐标与纵坐标均为整数的点）按其到原点的距离从近到远排成点列：（x1，y1），（x2，y2），（x3，y3），…，（xn，yn）．
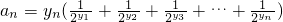，求数列{an}的前n项和Sn；
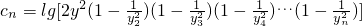，且数列{cn}的前n项和Tn，求T99．
所表示的平面区域为Dn，把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成一列点：(x1，y1)，(x2，y2)，(x3，y3)，…，(xn，yn)．
(λ为非零常数)，问是否存在整数λ，使得对任意n∈N*，都有an+1＞an.
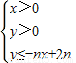所表示的平面区域为Dn，把Dn内的整点（横坐标与纵坐标均为整数的点）按其到原点的距离从近到远排成点列：（x1，y1），（x2，y2），（x3，y3），…，（xn，yn）．
，求数列{an}的前n项和Sn；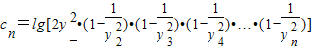
，且数列{cn}的前n项和Tn，求T99．
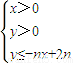所表示的平面区域为Dn，把Dn内的整点（横坐标与纵坐标均为整数的点）按其到原点的距离从近到远排成一列点：（x1，y1），（x2，y2），（x3，y4），…，（xn，yn）
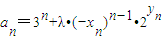（λ为非零常数），问是否存在整数λ，使得对任意n∈N*，都有an+1＞an．
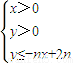所表示的平面区域为Dn，把Dn内的整点（横坐标与纵坐标均为整数的点）按其到原点的距离从近到远排成点列：（x1，y1），（x2，y2），（x3，y3），…，（xn，yn）．
，求数列{an}的前n项和Sn；
，且数列{cn}的前n项和Tn，求T99．