Question

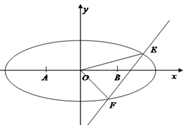
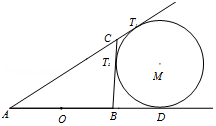
【题目】如图所示，在△ABC中，AB的中点为O，且OA=1，点D在AB的延长线上，且 ．固定边AB，在平面内移动顶点C，使得圆M与边BC，边AC的延长线相切，并始终与AB的延长线相切于点D，记顶点C的轨迹为曲线Γ．以AB所在直线为x轴，O为坐标原点如图所示建立平面直角坐标系．
（Ⅰ）求曲线Γ的方程；
（Ⅱ）设动直线l交曲线Γ于E、F两点，且以EF为直径的圆经过点O，求△OEF面积的取值范围．

Answer 1

【答案】解：（Ⅰ）依题意得AB=2，BD=1，设动圆M与边AC的延长线相切于T1 ， 与边BC相切于T2 ， 则AD=AT1 ， BD=BT2 ， CT1=CT2所以AD+BD=AT1+BT2=AC+CT1+BT2=AC+CT1+CT2=AC+BC=AB+2BD=4＞AB=2
所以点C轨迹Γ是以A，B为焦点，长轴长为4的椭圆，且挖去长轴的两个顶点．则曲线Γ的方程为 ．
（Ⅱ）由于曲线Γ要挖去长轴两个顶点，所以直线OE，OF斜率存在且不为0，所以可设直线

由 得 ， ，同理可得： ， ；
所以 ，
又OE⊥OF，所以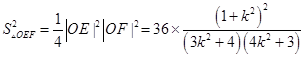
令t=k2+1，则t＞1且k2=t﹣1，所以 =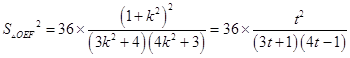
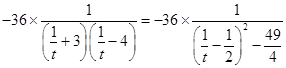
又 ，所以 ，所以 ，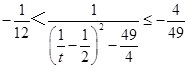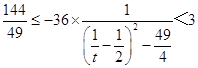
所以 ，所以 ，
所以△OEF面积的取值范围为 ．

【解析】（Ⅰ）确定点C轨迹Γ是以A，B为焦点，长轴长为4的椭圆，且挖去长轴的两个顶点，即可求曲线Γ的方程；（Ⅱ）可设直线 ，进而表示面积，即可求△OEF面积的取值范围．