题目内容
（本小题满分12分）
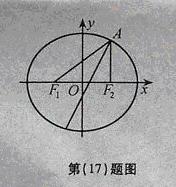椭圆
经过点
，对称轴为坐标轴，焦点
在
轴上，离心率
。
(Ⅰ)求椭圆的方程；
(Ⅱ)求
的角平分线所在直线的方程。
【命题意图】本题考查椭圆的定义及标准方程，椭圆的简单几何性质，直线的点斜式方程与一般方程，点到直线的距离公式等基础知识；考查解析几何的基本思想、综合运算能力.
【解题指导】（1）设椭圆方程为
，把点
代入椭圆方程，把离心率
用
表示，再根据
，求出
，得椭圆方程；（2）可以设直线l上任一点坐标为
，根据角平分线上的点到角两边距离相等得
.
解：（Ⅰ）设椭圆E的方程为
【规律总结】对于椭圆解答题，一般都是设椭圆方程为，根据题目满足的条件求出，得椭圆方程，这一问通常比较简单；（2）对于角平分线问题，利用角平分线的几何意义，即角平分线上的点到角两边距离相等得方程.
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
