题目内容



解法一:设Q
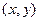 ,Q点不在原点,
,Q点不在原点,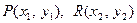
显然x,y不同是为零
①P点不在y轴时,即
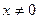 时
时∵R不在椭圆上
∴
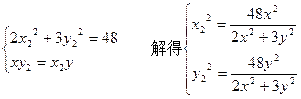
又∵
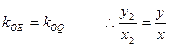
∵P点在直线l上,∴
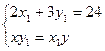
解得:
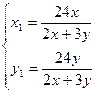
∵

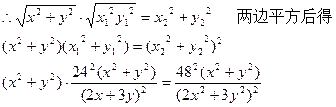
∵x、y不同时为零
∴
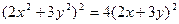
∵Q点与坐标原点O在直线l的同侧
∴
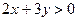
则:
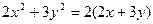
即:
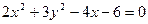
②P点在y轴上时,P(0,8)
k(0,4)
 可得Q(0,2),Q点满足这个方程
可得Q(0,2),Q点满足这个方程∴所求的轨迹方程是
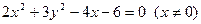
 |
∵
又∵

∴
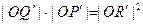
即
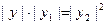
由题已知
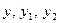 三个量同号
三个量同号∴
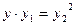
设射线OP方程为
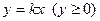
则
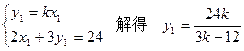
又R也在OP上,∴
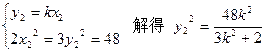
代入
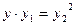 中
中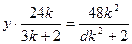
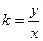
化简:
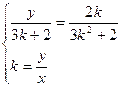
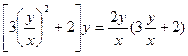
∵
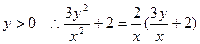
则
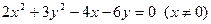 为所求的轨迹方程
为所求的轨迹方程本题动点Q的运动依赖于①P点的运动。② 这样两个关系,又O、Q、R、P、D点共线,可以把P点、R点的坐标分别用动点Q的坐标表示后一起代入③④⑤
这样两个关系,又O、Q、R、P、D点共线,可以把P点、R点的坐标分别用动点Q的坐标表示后一起代入③④⑤ 中去整理。化简得轨迹方程;另外也可以过Q、R、P三点分别做y轴的垂线,将
中去整理。化简得轨迹方程;另外也可以过Q、R、P三点分别做y轴的垂线,将 转化成这三点纵坐标的关系,再求轨迹方程。本题解法一仍是坐标代换法的一种形式,主要是将动点的相关点的坐标用动点坐标表示后,代入联系着它们的等式中,求出动点的轨迹方程,这里因P点在直线l:
转化成这三点纵坐标的关系,再求轨迹方程。本题解法一仍是坐标代换法的一种形式,主要是将动点的相关点的坐标用动点坐标表示后,代入联系着它们的等式中,求出动点的轨迹方程,这里因P点在直线l: 上运动,而该直线与y轴可以相交,当P点在y轴上时,R、Q也相对确定成为定值,所以在解决这个问题时,先两步,第一部P在直线l上,运动不在y轴时(完全是“动态”)情况,第二步必须再看P在y轴时Q点做为定点是否符合所求的轨迹方程。这正是容易被忽略的,必须注意。
上运动,而该直线与y轴可以相交,当P点在y轴上时,R、Q也相对确定成为定值,所以在解决这个问题时,先两步,第一部P在直线l上,运动不在y轴时(完全是“动态”)情况,第二步必须再看P在y轴时Q点做为定点是否符合所求的轨迹方程。这正是容易被忽略的,必须注意。
综上,在圆锥曲线的标准方程这部分内容中,应掌握的求曲线方程的基本方法。由于求曲线方程是平面解析几何两个主要内容之一,可以题型多,方法多。但因为坐标轴平移还没学到因而涉及到园锥曲线的一般式的问题后再讲。
 这样两个关系,又O、Q、R、P、D点共线,可以把P点、R点的坐标分别用动点Q的坐标表示后一起代入③④⑤
这样两个关系,又O、Q、R、P、D点共线,可以把P点、R点的坐标分别用动点Q的坐标表示后一起代入③④⑤ 中去整理。化简得轨迹方程;另外也可以过Q、R、P三点分别做y轴的垂线,将
中去整理。化简得轨迹方程;另外也可以过Q、R、P三点分别做y轴的垂线,将 转化成这三点纵坐标的关系,再求轨迹方程。本题解法一仍是坐标代换法的一种形式,主要是将动点的相关点的坐标用动点坐标表示后,代入联系着它们的等式中,求出动点的轨迹方程,这里因P点在直线l:
转化成这三点纵坐标的关系,再求轨迹方程。本题解法一仍是坐标代换法的一种形式,主要是将动点的相关点的坐标用动点坐标表示后,代入联系着它们的等式中,求出动点的轨迹方程,这里因P点在直线l: 上运动,而该直线与y轴可以相交,当P点在y轴上时,R、Q也相对确定成为定值,所以在解决这个问题时,先两步,第一部P在直线l上,运动不在y轴时(完全是“动态”)情况,第二步必须再看P在y轴时Q点做为定点是否符合所求的轨迹方程。这正是容易被忽略的,必须注意。
上运动,而该直线与y轴可以相交,当P点在y轴上时,R、Q也相对确定成为定值,所以在解决这个问题时,先两步,第一部P在直线l上,运动不在y轴时(完全是“动态”)情况,第二步必须再看P在y轴时Q点做为定点是否符合所求的轨迹方程。这正是容易被忽略的,必须注意。综上,在圆锥曲线的标准方程这部分内容中,应掌握的求曲线方程的基本方法。由于求曲线方程是平面解析几何两个主要内容之一,可以题型多,方法多。但因为坐标轴平移还没学到因而涉及到园锥曲线的一般式的问题后再讲。

练习册系列答案
相关题目
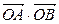 等于( )
等于( )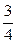
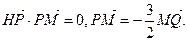
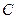 :
: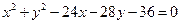 内有1点
内有1点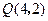 ,过
,过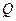 作直角
作直角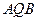 交圆于
交圆于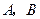 ,求动弦
,求动弦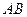 中点的轨迹方程.
中点的轨迹方程.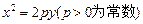 ,
,
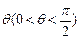 的直线交抛物线于
的直线交抛物线于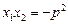
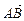 所成的比为
所成的比为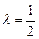 ,求直线AB的方程
,求直线AB的方程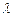 ,求
,求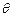 的函数关系式。
的函数关系式。 



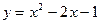
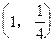
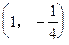
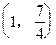
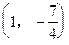
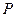 是曲线
是曲线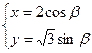 上一点,
上一点,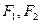 是该曲线的两个焦点,若
是该曲线的两个焦点,若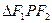 内角平分线的交点到三边上的距离为1,,则
内角平分线的交点到三边上的距离为1,,则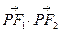 的值为
的值为 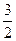
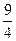
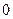
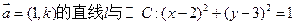 ,相交于M、N两点.
,相交于M、N两点.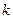 的取值范围;
的取值范围; 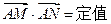 ;
;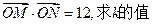 .
.