题目内容
若数列{an}为等差数列,a1>0,a2005+a2004>0,a2005•a2004<0,则使前n项和Sn>0的最大自然数n=
4008
4008
.分析:根据题意可知:此等差数列的1到2004项每一项都大于0,从第2005项开始每一项都小于0,然后利用等差数列的前n项和公式表示出前4008项的和与前4009项的和,分别利用等差数列的性质变形后,根据a2004+a2005>0与a2005<0,判断出前4008项的和为正与前4009项的和为负,即可求出满足题意的最大自然数n的值.
解答:解:由题意知:等差数列中,从第1项到第2004项是正数,且从第2005项开始为负数,
则S4008=2005(a1+a4008)=2005(a2004+a2005)>0,
S4009=
=4009a2005<0,
故n的最大值为4008.
故答案为:4008
则S4008=2005(a1+a4008)=2005(a2004+a2005)>0,
S4009=
| 4009(a1+a4009) |
| 2 |
故n的最大值为4008.
故答案为:4008
点评:此题考查了等差数列的性质,以及等差数列的求和公式.本小题结论可以推广成一般结论:等差数列中,a1>0,ak+ak+1>0,且akak+1<0,则使前n项和Sn>0的最大自然数n是2k.

练习册系列答案
相关题目
 时,
时,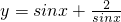 的最小值是
的最小值是 .
. =p(p为常数),则称数列{an}为“等差比”数列,p叫数列{an}的“公差比”.现给出如下命题:
=p(p为常数),则称数列{an}为“等差比”数列,p叫数列{an}的“公差比”.现给出如下命题: