题目内容
已知函数 ,其中函数
,其中函数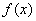 的图象在点
的图象在点 处的切线方程为
处的切线方程为 .
.
(Ⅰ)若 ,求函数
,求函数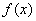 的解析式;
的解析式;
(Ⅱ)若 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围;
(Ⅲ)证明:
 .
.
 |
(Ⅰ) ,则有
,则有 ,解得
,解得

(Ⅱ)由(Ⅰ)知 ,令
,令
 ,则
,则 ,
,
(i)当 时,
时, 。
。
若 ,则
,则 ,
, 是减函数,所以
是减函数,所以 ,即
,即
故 在
在 上不恒成立.
上不恒成立.
(ii)当 时,
时, 。
。
若 ,则
,则 是增函数,所以
是增函数,所以 ,即
,即 故当
故当
时, .
.
综上所述,所求 的取值范围为
的取值范围为 。
。
(Ⅲ)解法一:由(Ⅱ)知当 时,有
时,有 。
。
令 有
有

且当 时,
时,
 。 令
。 令 有
有

 ,
,
将上述 个不等式依次相加,得
个不等式依次相加,得

整理得
解法二:用数学归纳法证明.
①当 时,左边
时,左边 ,右边
,右边 不等式成立.
不等式成立.
②假设当 时,不等式成立,就是
时,不等式成立,就是

那么

由(Ⅱ)知,当 时,有
时,有 。
。
令 有
有 。
。
令 ,得
,得



 。
。
这就是说,当 时,不等式也成立
时,不等式也成立
根据①和②,可知不等式对任何 都成立。
都成立。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的解集为是
的解集为是 ,
, 的值
的值 的解集。
的解集。
 且
且
 若
若
 则
则
 ______.
______.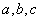 都在函数
都在函数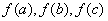 也是某个三角形的三边长,则称
也是某个三角形的三边长,则称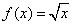 ; ②
; ②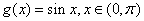 ;
; 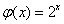 ; ④
; ④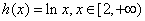 .
. ,
, ,则直线
,则直线 通过( )
通过( ) 满足
满足 ,若
,若 ,则
,则 ( )
( ) D.
D.
 ,
, ,则
,则 在复平面内对应的点在
在复平面内对应的点在