题目内容
设双曲线的-个焦点为F;虚轴的一个端点为B,如果直线FB与该双曲线的一条渐近线垂直,那么此双曲线的离心率为分析:由题意可得
•
=-1,c2-a2-ac=0,e2-e-1=0,解方程求得 e的值.
| b-0 |
| 0-c |
| b |
| a |
解答:解:由题意可得
•
=-1,∴ac=b2,∴c2-a2-ac=0,
∴e2-e-1=0,∴e=
,或 e=
(舍去),
故答案为:
.
| b-0 |
| 0-c |
| b |
| a |
∴e2-e-1=0,∴e=
1+
| ||
| 2 |
1-
| ||
| 2 |
故答案为:
1+
| ||
| 2 |
点评:本题考查双曲线的标准方程,以及双曲线的简单性质的应用,得到
•
=-1,是解题的关键.
| b-0 |
| 0-c |
| b |
| a |

练习册系列答案
相关题目
 的两个焦点分别为
的两个焦点分别为 ,离心率为
,离心率为 .
.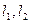 的方程;
的方程; 分别为
分别为 ,求线段
,求线段 的中点
的中点 的轨迹方程,并说明轨迹是什么曲线.
的轨迹方程,并说明轨迹是什么曲线. 的两个焦点为
的两个焦点为 ,P是双曲线上的一点,且
,P是双曲线上的一点,且 ,则△PF1 F2的面积等于( )
,则△PF1 F2的面积等于( ) B.8
B.8 D. 16
D. 16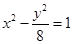 的两个焦点为
的两个焦点为 ,P是双曲线上的一点,且
,P是双曲线上的一点,且 ,则△PF1 F2的面积等于( )
,则△PF1 F2的面积等于( ) B.8
B.8 D. 16
D. 16