题目内容
已知数列{an}为等比数列,且a1+a2+a3=7,a解:由已知a1+a2+a3=7,a
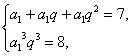 即
即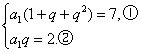
①÷②得![]() =
=![]() ,
,
即2q2-5q+2=0.解得q=2或q=![]() .
.
当q=2时,a1=1,∴an=2n-1.
当q=![]() 时,a1=4,∴an=23-n.
时,a1=4,∴an=23-n.
点评:首项a1和公比q是确定等比数列{an}最基本的量,而已知条件可转为关于a1与q的方程.

练习册系列答案
相关题目
题目内容
已知数列{an}为等比数列,且a1+a2+a3=7,a解:由已知a1+a2+a3=7,a
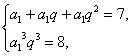 即
即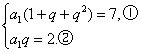
①÷②得![]() =
=![]() ,
,
即2q2-5q+2=0.解得q=2或q=![]() .
.
当q=2时,a1=1,∴an=2n-1.
当q=![]() 时,a1=4,∴an=23-n.
时,a1=4,∴an=23-n.
点评:首项a1和公比q是确定等比数列{an}最基本的量,而已知条件可转为关于a1与q的方程.
