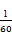题目内容
某中学在高一开设了数学史等4门不同的选修课,每个学生必须选修,且只能从中选一门。该校高一的3名学生甲、乙、丙对这4门不同的选修课的兴趣相同。
(1)求恰有2门选修课这3个学生都没有选择的概率;
(2)设随机变量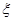 为甲、乙、丙这三个学生选修数学史这门课的人数,求
为甲、乙、丙这三个学生选修数学史这门课的人数,求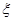 的分布列及期望,方差.
的分布列及期望,方差.
(1)求恰有2门选修课这3个学生都没有选择的概率;
(2)设随机变量
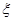 为甲、乙、丙这三个学生选修数学史这门课的人数,求
为甲、乙、丙这三个学生选修数学史这门课的人数,求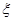 的分布列及期望,方差.
的分布列及期望,方差.(1) ;(2)详见解析.
;(2)详见解析.
 ;(2)详见解析.
;(2)详见解析.试题分析:(1)本题的总的基本事件的个数
 ,满足条件的事件数是
,满足条件的事件数是 ,代入公式得到结果.
,代入公式得到结果.(2)某一选择修课这3个学生选择的人数为0,1,2,3,属于二项分布,
 ,
,类似于前面所说,求出各种不同情况下对应的概率,写出分布列,算出期望.
(1)恰有2门选修课这3个学生都没有选择的概率:
 =
=
(Ⅲ)设数学史这门课这3个学生选择的人数为
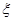 ,则
,则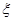 =0,1,2,3
=0,1,2,3 P (
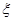 =" 0" ) =
=" 0" ) = P (
P (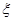 =" 1)" =
=" 1)" =
P (
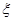 =" 2" ) =
=" 2" ) = P (
P (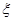 =" 3" ) =
=" 3" ) =
∴
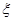 的分布列为:
的分布列为: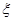 | 0 | 1 | 2 | 3 |
| P |  |  |  |  |
∴期望E
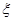 =np=
=np= ,
,

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目
 ,乙、丙去北京旅游的概率分别为
,乙、丙去北京旅游的概率分别为 ,
, ,假定三人的行动相互之间没有影响,那么这段时间内至少有1人去北京旅游的概率为( )
,假定三人的行动相互之间没有影响,那么这段时间内至少有1人去北京旅游的概率为( )