Question

（2013•嘉定区一模）如图，在直三棱柱ABC-A₁B₁C₁中，AB=2，AC=AA₁=4，∠ABC=90°．
（1）求三棱柱ABC-A₁B₁C₁的表面积S；
（2）求异面直线A₁B与AC所成角的大小（结果用反三角函数表示）．

Answer 1

分析：（1）利用S=2S_△ABC+S_侧，可求三棱柱ABC-A₁B₁C₁的表面积S；
（2）连接BC₁，确定∠BA₁C₁就是异面直线A₁B与AC所成的角（或其补角），在△A₁BC₁中，利用余弦定理可求结论．

解答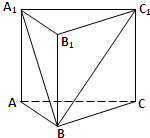：解：（1）在△ABC中，因为AB=2，AC=4，∠ABC=90°，所以BC=2

3

．…（1分）
S_△ABC=

1

2

AB×BC=2

3

．…（1分）
所以S=2S_△ABC+S_侧=4

3

+（2+2

3

+4）×4=24+12

3

．…（3分）
（2）连接BC₁，因为AC∥A₁C₁，所以∠BA₁C₁就是异面直线A₁B与AC所成的角（或其补角）．…（1分）
在△A₁BC₁中，A₁B=2

5

，BC₁=2

7

，A₁C₁=4，…（1分）
由余弦定理可得cos∠BA₁C₁=

5

10

，…（3分）
所以∠BA₁C₁=arccos

5

10

．…（1分）
即异面直线A₁B与AC所成角的大小为arccos

5

10

．…（1分）

点评：本题考查三棱柱的表面积，考查线线角，解题的关键是正确作出线线角，属于中档题．