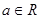题目内容
已知R上的不间断函数g(x)满足:
①当x>0时,g'(x)>0恒成立;
②对任意的x∈R都有g(x)=g(﹣x).又函数f(x)满足:对任意的x∈R,都有 成立,当
成立,当 时,f(x)=x3﹣3x.若关于x的不等式g[f(x)]≤
时,f(x)=x3﹣3x.若关于x的不等式g[f(x)]≤
g(a2﹣a+2)对x∈[﹣3,3]恒成立,则a的取值范围( )
①当x>0时,g'(x)>0恒成立;
②对任意的x∈R都有g(x)=g(﹣x).又函数f(x)满足:对任意的x∈R,都有
 成立,当
成立,当 时,f(x)=x3﹣3x.若关于x的不等式g[f(x)]≤
时,f(x)=x3﹣3x.若关于x的不等式g[f(x)]≤g(a2﹣a+2)对x∈[﹣3,3]恒成立,则a的取值范围( )
a≥1或a≤0

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
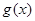 满足:①当
满足:①当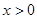 时,
时,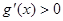 恒成立;②对任意的
恒成立;②对任意的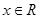 都有
都有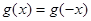 。又函数
。又函数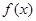 满足:对任意的
满足:对任意的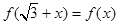 成立,当
成立,当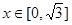 时,
时,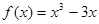 。若关于
。若关于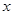 的不等式
的不等式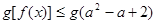 对
对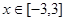 恒成立,则
恒成立,则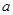 的取值范围( )
的取值范围( )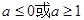 B.
B.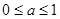 C.
C.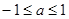 D.
D.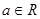
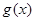 满足:①当
满足:①当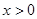 时,
时,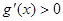 恒成立;②对任意的
恒成立;②对任意的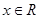 都有
都有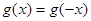 。又函数
。又函数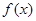 满足:对任意的
满足:对任意的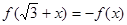 成立,当
成立,当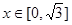 时,
时,
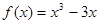 。若关于
。若关于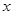 的不等式
的不等式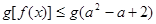 对
对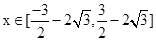 恒成立,则
恒成立,则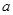 的取值范围( )
的取值范围( )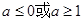 B.
B. 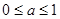 C.
C.
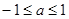 D.
D.