题目内容
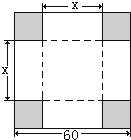 在边长为60cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
在边长为60cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
分析:先设箱底边长为xcm,则箱高h=
cm,得箱子容积,再利用导数的方法解决,应注意函数的定义域.
| 60-x |
| 2 |
解答: 解:设箱底边长为xcm,则箱高h=
解:设箱底边长为xcm,则箱高h=
cm,得箱子容积V(x)=x2h=
(0<x<60).
V′(x)=60x-
(0<x<60)
令 V′(x)=60x-
=0,
解得 x=0(舍去),x=40,
并求得V(40)=16 000
由题意可知,当x过小(接近0)或过大(接近60)时,箱子容积很小,因此,16 000是最大值
答:当x=40cm时,箱子容积最大,最大容积是16 000cm3
 解:设箱底边长为xcm,则箱高h=
解:设箱底边长为xcm,则箱高h=| 60-x |
| 2 |
| 60x2-x3 |
| 2 |
V′(x)=60x-
| 3x2 |
| 2 |
令 V′(x)=60x-
| 3x2 |
| 2 |
解得 x=0(舍去),x=40,
并求得V(40)=16 000
由题意可知,当x过小(接近0)或过大(接近60)时,箱子容积很小,因此,16 000是最大值
答:当x=40cm时,箱子容积最大,最大容积是16 000cm3
点评:(1)解有关函数最大值、最小值的实际问题,需要分析问题中各个变量之间的关系,找出适当的函数关系式,并确定函数的定义区间;所得结果要符合问题的实际意义.(2)根据问题的实际意义来判断函数最值时,如果函数在此区间上只有一个极值点,那么这个极值就是所求最值,不必再与端点值比较.(3)相当多有关最值的实际问题用导数方法解决较简单

练习册系列答案
相关题目
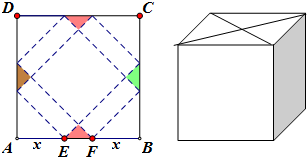 请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm).
请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm).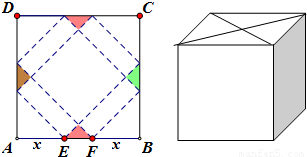 请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm).
请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm). 请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm).
请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm).
 分别表示|GE|、|EH|的长
分别表示|GE|、|EH|的长