题目内容
一个圆切直线l1：x－6y－10＝0于点P(4，－1)，且圆心在直线l2：5x－3y＝0上，求该圆的方程．
解法一：过点P(4，－1)且与直线l1：x－6y－10＝0垂直的直线的方程设为6x＋y＋c＝0.
把点P的坐标代入上式，得c＝－23，
即6x＋y－23＝0.
设所求圆的圆心为M(a，b)，
则满足6a＋b－23＝0.①
又由题设知圆心M在直线l2：5x－3y＝0上，
则5a－3b＝0.②
联立式①②，解得a＝3，b＝5，
即圆心M(3,5)，
因此半径r＝|PM|＝
＝
，
故所求圆的方程为(x－3)2＋(y－5)2＝37.
解法二(待定系数法)：设所求圆的方程为(x－a)2＋(y－b)2＝r2.
由题意，得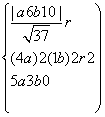
，得
.
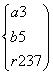故所求圆的方程为(x－3)2＋(y－5)2＝37.
练习册系列答案
快乐5加2金卷系列答案
相关题目