Question

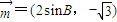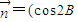
A，B，C是△ABC的内角，a，b，c分别是其对边，已知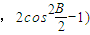，，且∥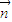，B为锐角，
（1）求B的大小；
（2）如果b=3，求△ABC的面积的最大值．

Answer 1

【答案】分析：（1）利用倍角公式和两角和的正弦公式及正弦函数的单调性即可求出；
（2）利用余弦定理和三角形的面积计算公式及基本不等式的性质即可求出．
解答：解：（1）∵，∴=0，化为，
∴2，即．
∵，∴，∴，解得．
（2）由余弦定理可得，
∴9=a²+b²-ac≥2ac-ac=ac，即ac≤9，
∴==．
即△ABC的面积的最大值为．
点评：熟练掌握正余弦定理、倍角公式、两角和的正余弦公式、三角形的面积计算公式及基本不等式的性质是解题的关键．