题目内容
如图,已知四棱锥S-ABCD中,△SAD是边长为a的正三角形,平面SAD⊥平面ABCD,四边形ABCD为菱形,∠DAB=60°,P为AD的中点,Q为SB的中点.
(Ⅰ)求证:PQ∥平面SCD;
(Ⅱ)求二面角B-PC-Q的大小.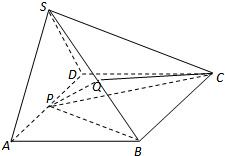
(Ⅰ)求证:PQ∥平面SCD;
(Ⅱ)求二面角B-PC-Q的大小.

证明:(1)证明取SC的中点R,连QR,DR.
由题意知:PD∥BC且PD=
BC;
QR∥BC且QP=
BC,∴QR∥PD且QR=PD.∴PQ∥DR,又PQ?面SCD,∴PQ∥面SCD.(6分)
(2)以P为坐标原点,PA为x轴,PB为y轴,PS为z轴建立空间直角坐标系,
则S(0,0,
a),B(0,
a,0),C(-a,
a,0),Q(0,
a,
a).
面PBC的法向量为
=(0,0,
a),设
=(x,y,z)为面PQC的一个法向量,
由
?
?
=(
,
,-
),
cos<
,
>=
=-
=-
,
∴二面角B-PC-Q的大小为arccos
.(12分)
由题意知:PD∥BC且PD=
| 1 |
| 2 |
QR∥BC且QP=
| 1 |
| 2 |
(2)以P为坐标原点,PA为x轴,PB为y轴,PS为z轴建立空间直角坐标系,
则S(0,0,
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 4 |
| ||
| 4 |
面PBC的法向量为
| PS |
| ||
| 2 |
| n |
由
|
|
| n |
| 3 |
| 2 |
| 3 |
| 3 |
cos<
| n |
| PS |
-
| ||||||||
|
| 2 | ||
|
| 2 |
| 11 |
| 11 |
∴二面角B-PC-Q的大小为arccos
2
| ||
| 11 |

练习册系列答案
相关题目
 如图,已知四棱锥S-ABCD的底面ABCD是边长为1的正方形,SA⊥平面ABCD,SA=2,E是侧棱SC上的一点.
如图,已知四棱锥S-ABCD的底面ABCD是边长为1的正方形,SA⊥平面ABCD,SA=2,E是侧棱SC上的一点.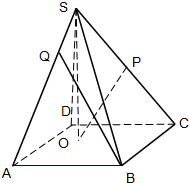 如图,已知四棱锥S-ABCD的底面是边长为4的正方形,S在底面上的射影O落在正方形ABCD内,SO的长为3,O到AB,AD的距离分别为2和1,P是SC的中点.
如图,已知四棱锥S-ABCD的底面是边长为4的正方形,S在底面上的射影O落在正方形ABCD内,SO的长为3,O到AB,AD的距离分别为2和1,P是SC的中点.
 (2008•湖北模拟)如图,已知四棱锥S-ABCD中,△SAD是边长为a的正三角形,平面SAD⊥平面ABCD,四边形ABCD为菱形,∠DAB=60°,P为AD的中点,Q为SB的中点.
(2008•湖北模拟)如图,已知四棱锥S-ABCD中,△SAD是边长为a的正三角形,平面SAD⊥平面ABCD,四边形ABCD为菱形,∠DAB=60°,P为AD的中点,Q为SB的中点. (2010•江西模拟)(如图)已知四棱锥S-ABCD的底面ABCD是菱形,将面SAB,SAD,ABCD 展开成平面后的图形恰好为一正三角形S'SC.
(2010•江西模拟)(如图)已知四棱锥S-ABCD的底面ABCD是菱形,将面SAB,SAD,ABCD 展开成平面后的图形恰好为一正三角形S'SC.