题目内容
下列判断正确的是
①函数y=|x-1|与y=
是同一函数;
②函数y=
在(1,+∞)内单调递增;
③函数f(x)=log2(
+x)是奇函数;
④函数y=-ex与y=e-x的图象关于坐标原点对称.
②③④
②③④
(把正确的序号都填上).①函数y=|x-1|与y=
|
②函数y=
| x-2 |
| x-1 |
③函数f(x)=log2(
| x2+1 |
④函数y=-ex与y=e-x的图象关于坐标原点对称.
分析:对于①,函数y=|x-1|与y=
不是同一函数,因为x=1时,y=
无定义;
②y=
=1-
在(1,+∞)内单调递增;
③由f(-x)+f(x)=0可判断③正确;
④函数y=-ex与y=e-x的图象关于坐标原点对称,正确.
|
|
②y=
| x-2 |
| x-1 |
| 1 |
| x-1 |
③由f(-x)+f(x)=0可判断③正确;
④函数y=-ex与y=e-x的图象关于坐标原点对称,正确.
解答:解:对于①因为x=1时,y=
无定义,
∴函数y=|x-1|与y=
不是同一函数,即可排除A;
对于②,y=
=1-
在(1,+∞)内单调递增,故②正确;
对于③,∵f(-x)+f(x)=log2(
-x)+log2(
+x)=log21=0,
∴f(-x)=-f(x),x∈R,
∴函数f(x)=log2(
+x)是奇函数,即③正确;
对于④,令g(x)=-ex,h(x)=e-x,
∵g(-x)=-e-x=-e-x=-h(x),
∴函数y=-ex与y=e-x的图象关于坐标原点对称,正确.
综上所述,②③④正确.
故答案为:②③④.
|
∴函数y=|x-1|与y=
|
对于②,y=
| x-2 |
| x-1 |
| 1 |
| x-1 |
对于③,∵f(-x)+f(x)=log2(
| x2+1 |
| x2+1 |
∴f(-x)=-f(x),x∈R,
∴函数f(x)=log2(
| x2+1 |
对于④,令g(x)=-ex,h(x)=e-x,
∵g(-x)=-e-x=-e-x=-h(x),
∴函数y=-ex与y=e-x的图象关于坐标原点对称,正确.
综上所述,②③④正确.
故答案为:②③④.
点评:本题考查函数的图象,考查函数奇偶性的判断与单调性的分析,考查函数的对称性,考查综合运用函数的性质解决问题的能力,属于中档题.

练习册系列答案
相关题目
已知函数y=sin(x-
)cos(x-
),则下列判断正确的是( )
| π |
| 12 |
| π |
| 12 |
A、此函数的最小正周期为2π,其图象的一个对称中心是(
| ||
B、此函数的最小正周期为π,其图象的一个对称中心是(
| ||
C、此函数的最小正周期为2π,其图象的一个对称中心是(
| ||
D、此函数的最小正周期为π,其图象的一个对称中心是(
|
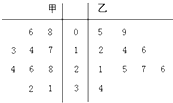 6、在如图所示的茎叶图中,若甲、乙两组数据的中位数分别为λ1,λ2,平均数分别为μ1,μ2,则下列判断正确的是( )
6、在如图所示的茎叶图中,若甲、乙两组数据的中位数分别为λ1,λ2,平均数分别为μ1,μ2,则下列判断正确的是( ) (2013•日照一模)如图,四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其中
(2013•日照一模)如图,四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其中