Question

已知正方体ABCD—A₁B₁C₁D₁中，E、F分别是D₁C₁、B₁C₁的中点，AC∩BD=P，A₁C₁∩EF=Q，求证：

(1)D、B、F、E四点共面；

(2)若直线A₁C交平面DBFE于点R，则P、Q、R三点共线.

Answer 1

(1)证法一:∵EF是△D₁B₁C₁的中位线,

∴EF∥B₁D₁.

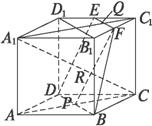
在正方体AC₁中，B₁D₁∥BD,

∴EF∥BD.

由公理3知EF、BD确定一个平面,

即D、B、F、E四点共面.

证法二:延长BF,CC₁交于点G,延长DE,CC₁交于点G′.

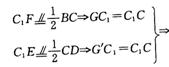G与G′重合DE,BF是相交直线D,B,F,E四点共面.

(2)证明:正方体ABCD—A₁B₁C₁D₁中，设A₁ACC₁确定的平面为α,设平面DBFE为β,

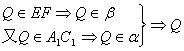∵为α、β的公共点.

同理,P亦为α、β的公共点,

∴R∈PQ,即P、Q、R三点共线.

点评:证明多点共线，可先由两点确定一直线，证其余点在直线上.要证点在一条直线上，只需证明这点是两平面的公共点，而直线是两个平面的交线，这是证点在直线上的常用方法.