题目内容
给出四个函数: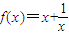 ,g(x)=3x+3-x,u(x)=x3,v(x)=sinx,其中满足条件:对任意实数x及任意正数m,有f(-x)+f(x)=0及f(x+m)>f(x)的函数为( )
,g(x)=3x+3-x,u(x)=x3,v(x)=sinx,其中满足条件:对任意实数x及任意正数m,有f(-x)+f(x)=0及f(x+m)>f(x)的函数为( )A.f(x)
B.g(x)
C.u(x)
D.v(x)
【答案】分析:根据题设条件,判定函数满足的条件是奇函数;同时是定义域上的增函数.
对于f(x),求单调区间来判断①是否满足;
对于g(x),判断函数在(-∞,0)上的单调性,可判断②是否满足;
对于u(x),根据幂函数的奇偶性与单调性可判定③是否满足;
对于v(x),根据正弦函数的单调区间可判断.
解答:解:对任意实数x及任意正数m,都有f(-x)+f(x)=0⇒函数为奇函数;满足f(x+m)>f(x)⇒函数是增函数;
对f(x),是奇函数,在(0,1)递减,∴不正确;
对g(x),是奇函数,(-∞,0)上递减,∴不正确;
对u(x),是奇函数,同时是R上的增函数,∴正确;
对v(x),是奇函数,正弦函数不是R上的增函数,∴不正确.
故选C.
点评:本题借助考查命题的真假判断,考查函数奇偶性的判断,考查函数单调性的判断与证明,属于中档题.
对于f(x),求单调区间来判断①是否满足;
对于g(x),判断函数在(-∞,0)上的单调性,可判断②是否满足;
对于u(x),根据幂函数的奇偶性与单调性可判定③是否满足;
对于v(x),根据正弦函数的单调区间可判断.
解答:解:对任意实数x及任意正数m,都有f(-x)+f(x)=0⇒函数为奇函数;满足f(x+m)>f(x)⇒函数是增函数;
对f(x),是奇函数,在(0,1)递减,∴不正确;
对g(x),是奇函数,(-∞,0)上递减,∴不正确;
对u(x),是奇函数,同时是R上的增函数,∴正确;
对v(x),是奇函数,正弦函数不是R上的增函数,∴不正确.
故选C.
点评:本题借助考查命题的真假判断,考查函数奇偶性的判断,考查函数单调性的判断与证明,属于中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
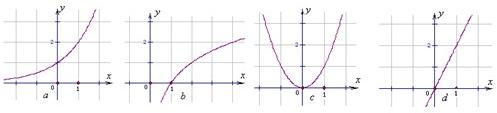

 ,g(x)=3x+3-x,u(x)=x3,v(x)=sinx,其中满足条件:对任意实数x及任意正数m,有f(-x)+f(x)=0及f(x+m)>f(x)的函数为
,g(x)=3x+3-x,u(x)=x3,v(x)=sinx,其中满足条件:对任意实数x及任意正数m,有f(-x)+f(x)=0及f(x+m)>f(x)的函数为