题目内容
【题目】在平面直角坐标系xOy中，已知P点到两定点D（﹣2，0），E（2，0）连线斜率之积为- 
．
（1）求证：动点P恒在一个定椭圆C上运动；
（2）过 
的直线交椭圆C于A，B两点，过O的直线交椭圆C于M，N两点，若直线AB与直线MN斜率之和为零，求证：直线AM与直线BN斜率之和为定值．
【答案】
（1）证明：设P（x，y），由题意可得kPDkPE=﹣ 
，
即有 
=﹣ ，
化为 
=1
（2）解：设过F的直线为x=my+ 
，
代入椭圆方程x2+2y2=4，
可得（2+m2）y2+2 my﹣2=0，
设A（x1，y1），B（x2，y2），
即有y1+y2=﹣ 
，y1y2=﹣ 
，
x1=my1+ ，x2=my2+ ，
由题意可得，过O的直线x=﹣my交椭圆C于M，N两点，
解得M（﹣ 
， 
），N（ ，﹣ ），
可得kAM+kBN=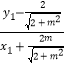 
+ 
，
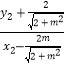通分后的分子=x2y1﹣ x2﹣ y1+x1y2+ x1+ y2+ 
=2my1y2+ （1+y2）+ （x1﹣x2）+ （y2﹣y1）+
=﹣ 
﹣ + （y1﹣y2）+ （y2﹣y1）+ =0．
即有直线AM与直线BN斜率之和为定值0．
【解析】（1）设P（x，y），由题意可得kPDkPE=﹣ ，运用直线的斜率公式，化简即可得到所求轨迹方程；（2）设过F的直线为x=my+ ，代入椭圆方程x2+2y2=4，设A（x1 ， y1），B（x2 ， y2），运用韦达定理，点满足直线方程，再由过O的直线x=﹣my交椭圆C于M，N两点，求得M，N的坐标，运用直线的斜率公式，化简整理，即可得到直线AM与直线BN斜率之和为定值0．
练习册系列答案
相关题目
