题目内容
函数y=tan 的单调区间是________.
的单调区间是________.
(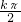 +
+ ,
,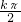 +
+ )(k∈Z)
)(k∈Z)
分析:利用诱导公式将y=tan( -2x)转化为y=-tan(2x-
-2x)转化为y=-tan(2x- ),利用正切函数的单调性即可求得答案.
),利用正切函数的单调性即可求得答案.
解答:∵y=tan( -2x)=-tan(2x-
-2x)=-tan(2x- ),
),
∴由kπ- <2x-
<2x- <kπ+
<kπ+ (k∈Z)得:
(k∈Z)得:
 +
+ <x<
<x< +
+ (k∈Z),
(k∈Z),
∴函数y=tan( -2x)的单调减区间为:(
-2x)的单调减区间为:( +
+ ,
, +
+ )(k∈Z)
)(k∈Z)
故答案为:( +
+ ,
, +
+ )(k∈Z)
)(k∈Z)
点评:本题考查复合三角函数的单调性,突出考查正切函数的单调性,考查诱导公式,将y=tan( -2x)转化为y=-tan(2x-
-2x)转化为y=-tan(2x- )是关键,属于中档题.
)是关键,属于中档题.
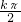 +
+ ,
,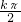 +
+ )(k∈Z)
)(k∈Z)分析:利用诱导公式将y=tan(
 -2x)转化为y=-tan(2x-
-2x)转化为y=-tan(2x- ),利用正切函数的单调性即可求得答案.
),利用正切函数的单调性即可求得答案.解答:∵y=tan(
 -2x)=-tan(2x-
-2x)=-tan(2x- ),
),∴由kπ-
 <2x-
<2x- <kπ+
<kπ+ (k∈Z)得:
(k∈Z)得: +
+ <x<
<x< +
+ (k∈Z),
(k∈Z),∴函数y=tan(
 -2x)的单调减区间为:(
-2x)的单调减区间为:( +
+ ,
, +
+ )(k∈Z)
)(k∈Z)故答案为:(
 +
+ ,
, +
+ )(k∈Z)
)(k∈Z)点评:本题考查复合三角函数的单调性,突出考查正切函数的单调性,考查诱导公式,将y=tan(
 -2x)转化为y=-tan(2x-
-2x)转化为y=-tan(2x- )是关键,属于中档题.
)是关键,属于中档题. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目