Question

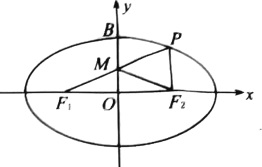
【题目】已知如图，椭圆：与直线交椭圆于，两点．

（Ⅰ）若直线经过椭圆的左焦点，交轴于点，且满足，.求证：为定值；

（Ⅱ）若，求面积的取值范围．

Answer 1

【答案】（Ⅰ）见解析； （Ⅱ）.

【解析】

（Ⅰ）设出直线方程，设出AB的坐标，直线方程代入椭圆方程，利用韦达定理结合，．即可证明：λ+μ为定值；（Ⅱ）当直线OA，OB分别与坐标轴重合时，易知．当直线OA，OB斜率存在且不为0时，设，设，，直线y＝kx代入椭圆C得到x2+2k2x2﹣2＝0，求出A，B坐标，表示出三角形的面积，利用换元法转化为二次函数求解三角形的面积的范围．

（Ⅰ）证明：由题设知直线斜率存在，设直线方程为，则.

设，，直线代入椭圆得，

所以，，

由，知，，.

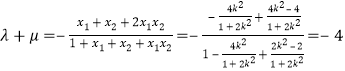（Ⅱ）当直线，分别与坐标轴重合时，易知.

当直线，斜率存在且不为0时，设：，：，

设，，直线代入椭圆得到，

所以，，

同理，，

，

令，

则 ，

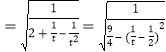因为，所以，

故，综上.