题目内容
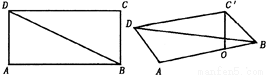
(理)如图,在矩形ABCD中,AB=3
,BC=3,沿对角线BD将△BCD折起,使点C移到点C',且C'在平面ABD的射影O恰好在AB上.
(1)求证:BC'⊥面ADC';
(2)求二面角A-BC'-D的大小;
(3)求直线AB和平面BC'D所成的角.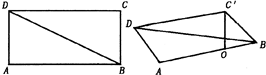
| 3 |
(1)求证:BC'⊥面ADC';
(2)求二面角A-BC'-D的大小;
(3)求直线AB和平面BC'D所成的角.

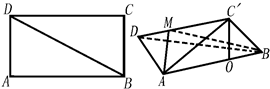
(理)(1)∵DA?平面ABD,
AB是BC‘在平面ABD内的射影,
DA⊥AB,
∴DA⊥BC’,BC‘⊥DC’,
∴BC‘⊥平面ADC’.…(4分)
(2)∵BC'⊥平面ADC',
∴
|
∴∠DC'A是二面角A-BC'-D的平面角…(6分)
∵BC‘⊥平面ABC’,
∴DA⊥BC‘,DA⊥AB,
∴DA⊥面ABC',
∴DA⊥AC’.…(7分)
在Rt△AC'D中,sin∠DC'A=
| DA |
| C′D |
| 3 | ||
3
|
| ||
| 3 |
所以,二面角A-BC'-D的大小为arcsin
| ||
| 3 |
(3)作AM⊥DC'于M,连接BM,
∵BC‘⊥面ADC’,
∴面ADC‘⊥面BDC’,
∵AM⊥DC‘,
∴AM⊥面BC'D,
∴∠ABM是AB与平面BC'D所成的角,…(10分)
在Rt△DAC'中,AM•DC'=AD•AC',
∴AM=
| AD•AC′ |
| DC′ |
3•3
| ||
3
|
| 6 |
在Rt△ABM中sin∠ABM=
| AM |
| AB |
| ||
3
|
| ||
| 3 |
所以,AB与平面BC'D所成的角为arcsin
| ||
| 3 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2004•宁波模拟)(理)如图,在矩形ABCD中,
(2004•宁波模拟)(理)如图,在矩形ABCD中,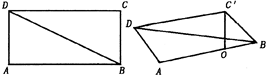 (理)如图,在矩形ABCD中,
(理)如图,在矩形ABCD中,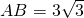 ,BC=3,沿对角线BD将△BCD折起,使点C移到点C',且C'在平面ABD的射影O恰好在AB上.
,BC=3,沿对角线BD将△BCD折起,使点C移到点C',且C'在平面ABD的射影O恰好在AB上.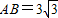 ,BC=3,沿对角线BD将△BCD折起,使点C移到点C',且C'在平面ABD的射影O恰好在AB上.
,BC=3,沿对角线BD将△BCD折起,使点C移到点C',且C'在平面ABD的射影O恰好在AB上.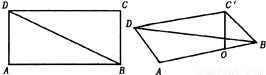
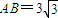 ,BC=3,沿对角线BD将△BCD折起,使点C移到点C',且C'在平面ABD的射影O恰好在AB上.
,BC=3,沿对角线BD将△BCD折起,使点C移到点C',且C'在平面ABD的射影O恰好在AB上.