题目内容

（2012•自贡三模）设O为坐标原点，A（-1，1），平面区域M为
x≥0
y≥0
1≤x+y≤3
，随机从区域M中抽取一整点P （横、纵坐标都是整数），则
OA
•
OP
＞0的概率是（　　）
分析：由
OA
•
OP
=-x+y＞0可得x＜y，作出不等式 组表示的平面区域，求出满足条件的整点的个数，然后求出满足
OA
•
OP
＞0的个数，可求
解答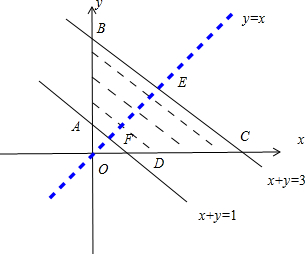：解：由题意可知，
OA
=（-1，1），
OP
=（x，y）
∴
OA
•
OP
=-x+y＞0
∴x＜y
作出不等式组
x≥0
y≥0
1≤x+y≤3
表示的平面区域，如图所示的四边形ABCD，区域内的整点有（0，1）（0，2）（0，3）（1，0）（1，1）（1，2）（2，0）（2，1）（3，0）共9个
满足x＜y的整点有（0，1）（0，2）（0，3）（1，2）共有4个
P=
4
9

故选D
点评：本题考查几何概型，几何概型的概率的值是通过长度、面积、和体积、的比值得到，本题是通过，满足条件的个数之比得到概率的值．
练习册系列答案
相关题目
（2012•自贡三模）对于三次函数f（x）=ax3+bx2+cx+d（a≠0），定义f′（x）是y=f（x）的导函数y=f′（x）的导函数，若方程f′（x）=0有实数解x0，则称点（x0，f（x0））为函数y=f（x）的“拐点”，可以发现，任何三次函数都有“拐点”，任何三次函数都有对称中心，且“拐点”就是对称中心，请你根据这一发现判断下列命题：
①任意三次函数都关于点（-
b
3a
，f（-
b
3a
））对称：
②存在三次函数f′（x）=0有实数解x0，点（x0，f（x0））为函数y=f（x）的对称中心；
③存在三次函数有两个及两个以上的对称中心；
④若函数g（x）=
1
3
x3-
1
2
x2-
5
12
，则，g（
1
2012
）+g（
2
2012
）+g（
3
2012
）+…+g（
2011
2012
）=-105.5．
其中正确命题的序号为
①②④
①②④
（把所有正确命题的序号都填上）．
（2012•自贡三模）已知G是△ABC的重心，且a
GA
+b
GB
+
3
c
GC
=
0
，其中a，b，c分别为角A、B、C的对边，则cosc=（　　）
（2012•自贡三模）在三棱锥A-BCD中，侧棱AB、AC、AD两两垂直，△ABC，△ACD，△ADB的面积分别为
2
2
，
3
2
，
6
2
，则三棱锥A-BCD的外接球的体积为
6
π
6
π
．
（2012•自贡三模）已知圆C：（x-a）2+（y-2）2=4（a＞0）及直线l：x-y+3=0，当直线l被C截得弦长为2
3
时，则a=
2
-1
2
-1
．
（2012•自贡三模）若(x2+
1
ax
)6的展开式中的常数项为
15
16
，则实数a
±2
±2
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网