题目内容
14.已知α为第二象限角,β为第一象限角,sinα=$\frac{3}{5}$,cosβ=$\frac{\sqrt{2}}{2}$(1)求cos2α的值;
(2)求tan(2α-β)的值.
分析 (1)原式利用二倍角的余弦函数公式化简,把sinα的值代入计算即可求出值;
(2)由题意求出cosα与sinβ的值,进而求出tanα与tanβ的值,求出tan2α的值,原式利用两角和与差的正切函数公式化简,把各自的值代入计算即可求出值.
解答 解:(1)∵sinα=$\frac{3}{5}$,
∴cos2α=1-2sin2α=1-2×$\frac{9}{25}$=$\frac{7}{25}$;
(2)∵α为第二象限角,β为第一象限角,sinα=$\frac{3}{5}$,cosβ=$\frac{\sqrt{2}}{2}$,
∴cosα=-$\sqrt{1-si{n}^{2}α}$=-$\frac{4}{5}$,sinβ=$\frac{\sqrt{2}}{2}$,
∴tanα=-$\frac{3}{4}$,tanβ=1,tan2α=$\frac{2tanα}{1-ta{n}^{2}α}$=$\frac{2×(-\frac{3}{4})}{1-\frac{9}{16}}$=-$\frac{24}{7}$,
则tan(2α-β)=$\frac{tan2α-tanβ}{1+tan2αtanβ}$=$\frac{-\frac{24}{7}-1}{1-\frac{24}{7}}$=$\frac{31}{17}$.
点评 此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
2.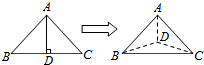 如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折
如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折
成互相垂直的两个平面后,某学生得出下列四个结论
①BD⊥AC;
②△BAC是等边三角形;
③三棱锥D-ABC是正三棱锥;
④平面ADC⊥平面ABC
其中正确的是( )
 如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折
如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论
①BD⊥AC;
②△BAC是等边三角形;
③三棱锥D-ABC是正三棱锥;
④平面ADC⊥平面ABC
其中正确的是( )
| A. | ①②④ | B. | ①②③ | C. | ②③④ | D. | ①③④ |
19.若θ是△ABC的一个内角,且sinθcosθ=$\frac{1}{8}$,则sinθ+cosθ=( )
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $-\frac{{\sqrt{5}}}{2}$ |
3.如图是函数y=f(x)的导函数y=f′(x)的图象,则下面判断正确的是( )


| A. | 在区间(-2,1)内f(x)是增函数 | B. | 在(1,3)内f(x)是减函数 | ||
| C. | 在(4,5)内f(x)是增函数 | D. | 在x=2时f(x)取到极小值 |