题目内容
等比数列{an}中,已知a1+a2+a3+a4=10,a5+a6+a7+a8=5,则数列{an}的前16项和S16为
- A.-50
- B.

- C.
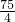
- D.-

C
分析:先利用已知a1+a2+a3+a4=10,a5+a6+a7+a8=5,求出q4= ;再利用整体代换思想求出后8项的和即可得到结论.
;再利用整体代换思想求出后8项的和即可得到结论.
解答:设等比数列的公比为q.
由a1+a2+a3+a4=10,
得a5+a6+a7+a8=q4(a1+a2+a3+a4)=10q4=5?q4= .
.
∴a9+a10+a11+a12+a13+a14+a15+a16
=q8(a1+a2+a3+a4)+q12(a1+a2+a3+a4)
=(q8+q12)(a1+a2+a3+a4)
=[ +
+ ]×10=
]×10= .
.
∴S16=10+5+ =
=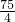 .
.
故选:C.
点评:本题主要考查等比数列的性质以及整体思想的应用.属于基础题目,在做题过程中计算要准确,即可做对.
分析:先利用已知a1+a2+a3+a4=10,a5+a6+a7+a8=5,求出q4=
 ;再利用整体代换思想求出后8项的和即可得到结论.
;再利用整体代换思想求出后8项的和即可得到结论.解答:设等比数列的公比为q.
由a1+a2+a3+a4=10,
得a5+a6+a7+a8=q4(a1+a2+a3+a4)=10q4=5?q4=
 .
.∴a9+a10+a11+a12+a13+a14+a15+a16
=q8(a1+a2+a3+a4)+q12(a1+a2+a3+a4)
=(q8+q12)(a1+a2+a3+a4)
=[
 +
+ ]×10=
]×10= .
.∴S16=10+5+
 =
=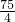 .
.故选:C.
点评:本题主要考查等比数列的性质以及整体思想的应用.属于基础题目,在做题过程中计算要准确,即可做对.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目