题目内容
下列说法中
①设定点F1(0,-3),F2(0,3),动点P(x,y)满足条件|PF1|+|PF2|=a(a>0),则动点P的轨迹是椭圆或线段;
②命题“每个指数函数都是单调函数”是全称命题,而且是真命题.
③离心率为
,长轴长为8的椭圆标准方程为
+
=1;
④若3<k<4,则二次曲线
+
=1的焦点坐标是(±1,0).
其中正确的为
①设定点F1(0,-3),F2(0,3),动点P(x,y)满足条件|PF1|+|PF2|=a(a>0),则动点P的轨迹是椭圆或线段;
②命题“每个指数函数都是单调函数”是全称命题,而且是真命题.
③离心率为
| 1 |
| 2 |
| x2 |
| 16 |
| y2 |
| 12 |
④若3<k<4,则二次曲线
| x2 |
| 4-k |
| y2 |
| 3-k |
其中正确的为
②④
②④
(写出所有真命题的序号)分析:根据动点P(x,y)满足条件|PF1|+|PF2|=a,当a<6,动点P的轨迹不存在,当a=6,动点P的轨迹为线段,当a>6,动点P的轨迹为椭圆,可判断①的真假;
根据指数函数的定义及其性质,可分析②的真假;
根据离心率为
,长轴长为8,分焦点在x轴上和焦点在y轴上两种情况分别求出椭圆的标准方程,可判断③的真假;
根据3<k<4,可分析出二次曲线
+
=1的图象形状及焦点位置,进而判断④的真假;
根据指数函数的定义及其性质,可分析②的真假;
根据离心率为
| 1 |
| 2 |
根据3<k<4,可分析出二次曲线
| x2 |
| 4-k |
| y2 |
| 3-k |
解答:解:①中,若a<6,则动点P的轨迹不存在,故①错误;
形如y=ax(a>0,a≠1)的函数为指数函数,且当a>1时为增函数,当0<a<1时为减函数,故命题“每个指数函数都是单调函数”是全称命题,而且是真命题正确,故②正确;
离心率为
,长轴长为8的椭圆标准方程为
+
=1或
+
=1,③错误;
若3<k<4,则二次曲线
+
=1为双曲线,则c2=(4-k)+(k-3)=1,此时c=1,且焦点在x轴上,故焦点坐标是(±1,0),故④正确
故答案为:②④
形如y=ax(a>0,a≠1)的函数为指数函数,且当a>1时为增函数,当0<a<1时为减函数,故命题“每个指数函数都是单调函数”是全称命题,而且是真命题正确,故②正确;
离心率为
| 1 |
| 2 |
| x2 |
| 16 |
| y2 |
| 12 |
| x2 |
| 12 |
| y2 |
| 16 |
若3<k<4,则二次曲线
| x2 |
| 4-k |
| y2 |
| 3-k |
故答案为:②④
点评:本题以命题的真假判断为载体考查了圆锥曲线的定义,性质及方程,考查了指数函数的定义及性质,熟练掌握圆锥曲线的定义,性质,标准方程是解答的关键.

练习册系列答案
相关题目
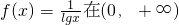 是减函数;
是减函数;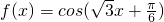 ,则f(x)+f'(x)是奇函数;
,则f(x)+f'(x)是奇函数;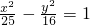 的一个焦点到渐近线的距离是5;
的一个焦点到渐近线的距离是5; 是减函数;
是减函数; ,则f(x)+f'(x)是奇函数;
,则f(x)+f'(x)是奇函数; 的一个焦点到渐近线的距离是5;
的一个焦点到渐近线的距离是5;